题目内容
设x、y满足约束条件:
,则Z=x+3y的最大值为 .
|
考点:分段函数的应用
专题:不等式的解法及应用
分析:先由约束条件画出可行域,再求出可行域各个角点的坐标,将坐标逐一代入目标函数,验证即得答案.
解答:
解:如图即为满足
的可行域,

由图易得:当x=
,y=
时
z=x+3y的最大值为
,
故答案为
|

由图易得:当x=
| 4 |
| 3 |
| 4 |
| 3 |
z=x+3y的最大值为
| 16 |
| 3 |
故答案为
| 16 |
| 3 |
点评:在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知双曲线的中心在坐标原点,焦点在x轴上,离心率是
,则该双曲线的渐近线方程是( )
| 2 |
A、y=±
| ||||
B、y=±
| ||||
| C、y=±x | ||||
D、y=±
|
已知a≥1,f(x)=x3+3|x-a|,若函数f(x)在[-1,1]上的最大值和最小值分别记为M、m,则M-m的值为 C( )
| A、8 |
| B、-a3-3a+4 |
| C、4 |
| D、-a3+3a+2 |
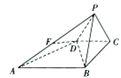 如图所示,已知四棱锥P=ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足PF=λPA.
如图所示,已知四棱锥P=ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足PF=λPA.