题目内容
5.直线l:xsin30°+ycos150°+1=0的倾斜角为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 化直线的一般式方程为斜截式,利用诱导公式变形,则直线的倾斜角可求.
解答 解:由xsin30°+ycos150°+1=0得到:
y=-$\frac{xsin30°+1}{cos150°}$=-$\frac{xsin30°+1}{-cos30°}$=tan30°x+$\frac{1}{cos30°}$,
则直线l:xsin30°+ycos150°+1=0的倾斜角为30°.
故选:A.
点评 本题考查直线的倾斜角,考查了直线的倾斜角与斜率的关系,是基础题.

练习册系列答案
相关题目
15.函数$f(x)=\sqrt{x+1}+{log_{2016}}(2-x)$的定义域为( )
| A. | (-2,1] | B. | [1,2] | C. | [-1,2) | D. | (-1,2) |
16.在极坐标系中,点(1,0)与点(2,π)的距离为( )
| A. | 1 | B. | 3 | C. | $\sqrt{1+{π^2}}$ | D. | $\sqrt{9+{π^2}}$ |
17.曲线y=-$\frac{1}{x}$在(1,-1)处的切线的斜率为( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
14.已知双曲线方程为x2-y2=4,过点A(3,1)作直线l与该双曲线交于M,N两点,若点A恰好为MN中点,则直线l的方程为( )
| A. | y=3x-8 | B. | y=-3x+8 | C. | y=3x-10 | D. | y=-3x+10 |
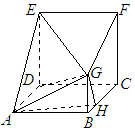 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH