题目内容
已知数列{an}满足an=an-1-an-2(n≥3,n∈N*),它的前n项和为Sn.若S9=6,S10=5,则a1的值为( )
| A、-2 | B、-1 | C、1 | D、2 |
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:根据数列的递推公式求出数列{an}是周期为6的周期数列,即可得到结论.
解答:
解:∵an=an-1-an-2(n≥3,n∈N*),
∴an+1=an-an-1(n≥3,n∈N*),即an+1=an-an-1=an-1-an-2-an-1=-an-2,
∴an+3=-an,即an+6=an,
∴数列{an}是周期为6的周期数列,
∵S9=6,S10=5,
∴a10=S10-S9=5-6=-1,
则a10=a4=-a1=-1,
∴a1=1,
故选C.
∴an+1=an-an-1(n≥3,n∈N*),即an+1=an-an-1=an-1-an-2-an-1=-an-2,
∴an+3=-an,即an+6=an,
∴数列{an}是周期为6的周期数列,
∵S9=6,S10=5,
∴a10=S10-S9=5-6=-1,
则a10=a4=-a1=-1,
∴a1=1,
故选C.
点评:本题主要考查数列项的计算,根据条件求出{an}是周期为6的周期数列是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
在△ABC中,已知a2tanB=b2tanA,则△ABC该的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、正三角形 |
| D、等腰或直角三角形 |
函数y=
cos2x+sinxcosx(-
)的周期是( )
| 3 |
| ||
| 2 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
已知函数f(x)=
.设a=log20.8,则f(f(a))的值等于( )
|
| A、1 | B、2 | C、-1 | D、-2 |
已知圆C:(x-a)2+(y-2)2=4(a>0)及直线l:x-y+3=0.当直线l被圆C截得的弦长为2
时,则a的值为( )
| 2 |
| A、1 | B、1或3 |
| C、-3 | D、1或-3 |
二项式(2x2-
)6的展开式中第4项的系数是( )
| 1 | |||
|
| A、20 | B、60 |
| C、-160 | D、160 |
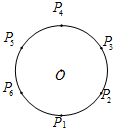 如图,设P1,P2,…,P6为单位圆上逆时针均匀分布的六个点.现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量S.
如图,设P1,P2,…,P6为单位圆上逆时针均匀分布的六个点.现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量S.