题目内容
9.已知双曲线C的渐近线方程为y=±x,一条准线方程为$x=\frac{{\sqrt{2}}}{2}$.(1)求双曲线C的方程;
(2)设过点M(-2,0)的直线l交双曲线C于A、B两点,并且三角形OAB的面积为2$\sqrt{3}$,求直线l的方程;
(3)在(2)中是否存在这样的直线l,使OA⊥OB?若存在,求直线l的方程;若不存在,请说明理由.
分析 (1)利用已知条件列出方程求出,a、b、c,即可得到双曲线方程.
(2)设出直线方程,与双曲线联立,利用三角形的面积求解直线方程即可.
(3)利用(2)通过直线垂直,斜率乘积为:-1.列出方程求解即可.
解答 解:(1)双曲线C的渐近线方程为y=±x,一条准线方程为$x=\frac{{\sqrt{2}}}{2}$.
可得a=b,$\frac{{a}^{2}}{c}$=$\frac{\sqrt{2}}{2}$,$\frac{c}{a}=\sqrt{2}$,解得,a=b=1,c=$\sqrt{2}$.
双曲线的方程为:x2-y2=1.
(2)设直线方程为:x=my-2,
由题意可得:$\left\{\begin{array}{l}{x=my-2}\\{{x}^{2}-{y}^{2}=1}\end{array}\right.$,
可得(m2-1)y2-4my+3=0,可得:y1+y2=$\frac{4m}{{m}^{2}-1}$,y1y2=$\frac{3}{{m}^{2}-1}$,
|y1-y2|=$\sqrt{\frac{16{m}^{2}-12{m}^{2}+12}{({m}^{2}-1)^{2}}}$=$\frac{\sqrt{12+4{m}^{2}}}{|{m}^{2}-1|}$,
三角形OAB的面积为2$\sqrt{3}$,可得:$\frac{1}{2}×2×$$\frac{\sqrt{12+4{m}^{2}}}{|{m}^{2}-1|}$=$2\sqrt{3}$,解得m=±$\frac{\sqrt{21}}{3}$.
直线l的方程:x=±$\frac{\sqrt{21}}{3}$y-2.
(3)由(2)可知y1y2=$\frac{3}{{m}^{2}-1}$,
x1x2=(my1-2)(my2-2)=m2y1y2-2m(y1+y2)+4=$\frac{3{m}^{2}}{{m}^{2}-1}-\frac{8{m}^{2}}{{m}^{2}-1}+4$=$\frac{-{m}^{2}-4}{{m}^{2}-1}$,
如果OA⊥OB,可得:$\frac{\frac{3}{{m}^{2}-1}}{\frac{-{m}^{2}-4}{{m}^{2}-1}}=-1$,
解得:m2=-1,
直线不存在.
点评 本题考查直线椭圆双曲线的位置关系的综合应用,考查分析问题解决问题的能力,转化思想的应用.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
 B.
B. C.
C.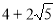 D.
D.