题目内容
4.设a、b、c∈R+,且a+b+c=1.(Ⅰ)求证:2ab+bc+ca+$\frac{{c}^{2}}{2}$$≤\frac{1}{2}$;
(Ⅱ)求证:$\frac{{a}^{2}+{c}^{2}}{b}+\frac{{b}^{2}+{a}^{2}}{c}+\frac{{c}^{2}+{b}^{2}}{a}≥2$.
分析 (Ⅰ)作差法化简1-2(2ab+bc+ca+$\frac{{c}^{2}}{2}$)=(a+b+c)2-(4ab+2bc+2ca+c2),从而证明;
(Ⅱ)易知$\frac{{a}^{2}}{b}$+b≥2a,$\frac{{c}^{2}}{b}$+b≥2c,$\frac{{b}^{2}}{c}$+c≥2b,$\frac{{a}^{2}}{c}$+c≥2a,$\frac{{c}^{2}}{a}$+a≥2c,$\frac{{b}^{2}}{a}$+a≥2b;从而证明.
解答 证明:(Ⅰ)∵1-2(2ab+bc+ca+$\frac{{c}^{2}}{2}$)
=(a+b+c)2-(4ab+2bc+2ca+c2)
=a2+b2-2ab=(a-b)2≥0,
∴2(2ab+bc+ca+$\frac{{c}^{2}}{2}$)≤1,
∴2ab+bc+ca+$\frac{{c}^{2}}{2}$$≤\frac{1}{2}$;
(Ⅱ)∵$\frac{{a}^{2}}{b}$+b≥2a,$\frac{{c}^{2}}{b}$+b≥2c,$\frac{{b}^{2}}{c}$+c≥2b,$\frac{{a}^{2}}{c}$+c≥2a,$\frac{{c}^{2}}{a}$+a≥2c,$\frac{{b}^{2}}{a}$+a≥2b;
∴$\frac{{a}^{2}}{b}$+b+$\frac{{c}^{2}}{b}$+b+$\frac{{b}^{2}}{c}$+c+$\frac{{a}^{2}}{c}$+c+$\frac{{c}^{2}}{a}$+a+$\frac{{b}^{2}}{a}$+a≥4(a+b+c),
即$\frac{{a}^{2}+{c}^{2}}{b}$+$\frac{{b}^{2}+{c}^{2}}{a}$+$\frac{{a}^{2}+{b}^{2}}{c}$+2(a+b+c)≥4(a+b+c),
故$\frac{{a}^{2}+{c}^{2}}{b}$+$\frac{{b}^{2}+{c}^{2}}{a}$+$\frac{{a}^{2}+{b}^{2}}{c}$≥2.
点评 本题考查不等式的证明方法的应用,应用了作差法.

| A. | [-$\frac{1}{3}$,$\frac{1}{5}$] | B. | [-$\frac{1}{3}$,1] | C. | (-∞,-$\frac{1}{3}$]∪[$\frac{1}{5}$,+∞) | D. | (-∞,-$\frac{1}{3}$]∪[1,+∞) |
| 报名参加学科竞赛 | 未报名参加学科竞赛 | |
| 报名参加自主招生 | 2 | 4 |
| 未报名参加自主招生 | 6 | 28 |
(2)从报名参加自主招生的同学中任取2人,求恰好1人两项都报名的概率.
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
 与圆
与圆 的位置关系为( )
的位置关系为( )
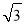 B.
B.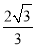 C.
C.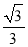 D.
D.