题目内容
某校甲、乙两个班级各有5名编号为1，2，3，4，5的学生进行投篮练习，每人投10次，投中的次数如下表：
则以上两组数据的方差中较小的一个为S2，则S2=（ ）
| 学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲班 | 6 | 7 | 7 | 8 | 7 |
| 乙班 | 6 | 7 | 6 | 7 | 9 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点：极差、方差与标准差
专题：概率与统计
分析：把表格中的数据分别代入平均数公式、方差公式，求出甲、乙两个班级的平均数、方差，再比较即可．
解答：
解：由题意得，
=
=7，
s甲2=
[(6-7)2+(7-7)2+(7-7)2+(8-7)2+(7-7)2]=
，
=
=7，
s乙2=
[(6-7)2+(7-7)2+(6-7)2+(7-7)2+(9-7)2]=
，
所以两组数据的方差中较小的一个为：
，
故选：A．
. |
| x甲 |
| 6+7+7+8+7 |
| 5 |
s甲2=
| 1 |
| 5 |
| 2 |
| 5 |
. |
| x乙 |
| 6+7+6+7+9 |
| 5 |
s乙2=
| 1 |
| 5 |
| 6 |
| 5 |
所以两组数据的方差中较小的一个为：
| 2 |
| 5 |
故选：A．
点评：本题考查平均数公式、方差公式，以及计算能力．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=
，若方程f（x）=a有四个不同的解x1，x2，x3，x4，且x1＜x2＜x3＜x4，则（x1+x2）+
+
的取值范围是（ ）
|
| 1 |
| x3 |
| 1 |
| x4 |
A、[0，
| ||
B、(0 ，
| ||
C、[0，
| ||
| D、[0，1） |
如图，直四棱柱ABCD-A1B1C11中，AB∥CD，AD⊥AB，AB=2，AD=已知f（x）为R上的增函数，且f（log2x）＞f（1），则x的取值范围为（ ）
| A、（2，+∞） | ||
B、（0，
| ||
C、（
| ||
| D、（0，1）∪（2，+∞） |
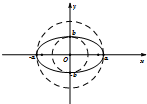圆锥曲线中不同曲线的性质都是有一定联系的，比如圆可以看成特殊的椭圆，所以很多圆的性质结论可以类比到椭圆，例如；如图所示，椭圆C：