题目内容
 已知梯形ABCD,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD,AD∥BC,∠ABC=∠BAD=| π |
| 2 |
(1)G是BC上的一点,且BD⊥EG,若x=3,求三棱锥B-AEG的体积;
(2)当x取何值时,三棱锥D-BCF的体积是最大值,最大值是多少.
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:(1)运用面面垂直的性质定理,可得AE⊥面EBCF,作DH⊥EF于H,连BH,GH,证得EG⊥BH,再由解直角三角形求得BG,再由VB-AEG=VA-BEG运用体积公式,即可得到;
(2)由面面垂直性质定理证出AE⊥面EBCF,结合(1)知AE=DH,利用锥体体积公式可得VF-BCD,利用二次函数的图象与性质可得当x=2时,体积有最大值.
(2)由面面垂直性质定理证出AE⊥面EBCF,结合(1)知AE=DH,利用锥体体积公式可得VF-BCD,利用二次函数的图象与性质可得当x=2时,体积有最大值.
解答:
 解:(1)∵AE⊥EF,面AEFD⊥面EBCF,面AEFD∩面EBCF=EF,
解:(1)∵AE⊥EF,面AEFD⊥面EBCF,面AEFD∩面EBCF=EF,
∴AE⊥面EBCF,
作DH⊥EF于H,连BH,
∵平面AEFD⊥平面EBCF,平面AEFD∩平面EBCF=EF,DH⊥EF
∴DH⊥平面EBCF,即DH⊥EG,
由于BD⊥EG,则EG⊥平面BDH,EG⊥BH,
在直角三角形EBG中,tan∠EGB=
=
,
在直角三角形EBH中,tan∠EHB=
=
,
由EG⊥BH,可得,tan∠EGB•tan∠EHB=1,即有BG=
.
则三棱锥B-AEG的体积为VB-AEG=VA-BEG
=
•AE•S△BEG=
•3•
•1•
=
;
(2)∵AE⊥EF,面AEFD⊥面EBCF,面AEFD∩面EBCF=EF,
∴AE⊥面EBCF,
由(1)知DH⊥平面EBCF,可得AE∥DH,AE=DH,
∴VD-BFC=
S△BFC•DH
=
S△BFC•DH
=
•
•4•(4-x)•x=-
(x-2)2+
≤
,
因此,当且仅当x=2时,f(x)有最大值为
.
 解:(1)∵AE⊥EF,面AEFD⊥面EBCF,面AEFD∩面EBCF=EF,
解:(1)∵AE⊥EF,面AEFD⊥面EBCF,面AEFD∩面EBCF=EF,∴AE⊥面EBCF,
作DH⊥EF于H,连BH,
∵平面AEFD⊥平面EBCF,平面AEFD∩平面EBCF=EF,DH⊥EF
∴DH⊥平面EBCF,即DH⊥EG,
由于BD⊥EG,则EG⊥平面BDH,EG⊥BH,
在直角三角形EBG中,tan∠EGB=
| EB |
| BG |
| 1 |
| BG |
在直角三角形EBH中,tan∠EHB=
| EB |
| EH |
| 1 |
| 2 |
由EG⊥BH,可得,tan∠EGB•tan∠EHB=1,即有BG=
| 1 |
| 2 |
则三棱锥B-AEG的体积为VB-AEG=VA-BEG
=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)∵AE⊥EF,面AEFD⊥面EBCF,面AEFD∩面EBCF=EF,
∴AE⊥面EBCF,
由(1)知DH⊥平面EBCF,可得AE∥DH,AE=DH,
∴VD-BFC=
| 1 |
| 3 |
=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
因此,当且仅当x=2时,f(x)有最大值为
| 8 |
| 3 |
点评:本题给出平面图形的翻折问题,在所得几何体中证明线线垂直并求三棱锥体积的最大值,着重考查了空间线面垂直、面面垂直的判定与性质、锥体体积和二次函数的图象与性质等知识,属于中档题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
“a=-1”是“(a-i)2”为纯虚数的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
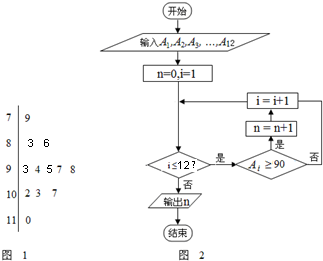 图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到12次的考试成绩依次记为A1,A2,…,A12.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )
图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到12次的考试成绩依次记为A1,A2,…,A12.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( )| A、8 | B、9 | C、10 | D、11 |
曲线y=1-
在点(-1,-1)处的切线方程为( )
| 2 |
| x+2 |
| A、y=2x+1 |
| B、y=2x-1 |
| C、y=-2x-3 |
| D、y=-2x-2 |