题目内容
已知椭圆C的左,右焦点分别为F1(-
,0),F2(
,0),且该椭圆过点(-1,
).
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知定点A(1,
),过原点O的直线l与曲线C交于M,N两点,求△MAN面积的最大值.
| 3 |
| 3 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知定点A(1,
| 1 |
| 2 |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据椭圆的结合性质求解得出a2=4,b2=1,即可得出方程.
(Ⅱ)分类①直线l的斜率不存在时;
②直线l的斜率存在时,△MAN面积:
×|MN|•d=
,转化为S△MNA的平方为:
=1-
利用基本不等式求解得出最大值.
(Ⅱ)分类①直线l的斜率不存在时;
②直线l的斜率存在时,△MAN面积:
| 1 |
| 2 |
2|k-
| ||
|
| 4k2-4k+1 |
| 1+4k2 |
| 4 | ||
4k+
|
解答:
解:(Ⅰ)∵椭圆C的左,右焦点分别为F1(-
,0),F2(
,0),
∴c=
,
∵该椭圆过点(-1,
).
∴
+
=1,a2=b2+3,
∴椭圆C的方程:
+y2=1.
(Ⅱ)①直线l的斜率不存在时,S△MNA=1,
②直线l的斜率存在时,
设直线l的方程y=kx,与椭圆C交与M(x1,y1),N(x2,y2),
联立方程组得出:|MN|=4
,
定点A(1,
)到直线l的距离d=
,
∴S△MAN面积:
×|MN|•d=
,
∴S△MNA的平方为:
=1-
,
∴当k=-
时,S△MNA的平方最大,
故△MAN面积的最大值为:
.
| 3 |
| 3 |
∴c=
| 3 |
∵该椭圆过点(-1,
| ||
| 2 |
∴
| 1 |
| a2 |
| ||
| b2 |
∴椭圆C的方程:
| x2 |
| 4 |
(Ⅱ)①直线l的斜率不存在时,S△MNA=1,
②直线l的斜率存在时,
设直线l的方程y=kx,与椭圆C交与M(x1,y1),N(x2,y2),
联立方程组得出:|MN|=4
|
定点A(1,
| 1 |
| 2 |
|k-
| ||
|
∴S△MAN面积:
| 1 |
| 2 |
2|k-
| ||
|
∴S△MNA的平方为:
| 4k2-4k+1 |
| 1+4k2 |
| 4 | ||
4k+
|
∴当k=-
| 1 |
| 2 |
故△MAN面积的最大值为:
| 2 |
点评:本题考察了圆锥曲线与直线的位置关系,求解方程,利用韦达定理求解弦长,面积,转化为函数求解,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知梯形ABCD,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD,AD∥BC,∠ABC=∠BAD=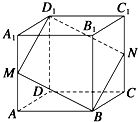 如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )
如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN,则四边形D1MBN在正方体各个面上的正投影图形中,不可能出现的是( )