题目内容
14.若an=2n-1+1(n∈N*),则33是数列{an}的第6项.分析 题目给出了一个数列的通项公式,判断33是这个数列的第几项,直接用33替换通项公式中的an,求解n的值即可.
解答 解:由题意可得:an=2n-1+1=33,
解得n=6,
故答案为:6.
点评 本题考查了数列的概念及简单表示法,考查了在通项公式给出的前提下由项求项数,是基础的计算题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
5.在一次抽奖活动中,8张奖券中有一、二、三等奖各1张,其余5张无奖.甲、乙、丙、丁四名顾客每人从中抽取2张,则不同的获奖情况有( )
| A. | 24种 | B. | 36种 | C. | 60种 | D. | 96种 |
2.已知sin(α+$\frac{π}{3}$)+sinα=-$\frac{4\sqrt{3}}{5}$.-$\frac{π}{2}$<α<0,则sin(-α+$\frac{5π}{6}$)等于( )
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
6.已知向量$\overrightarrow a=(2,m)$,$\overrightarrow b=(m,2)$,若$\overrightarrow a∥\overrightarrow b$,则实数m等于( )
| A. | -2 | B. | 2 | C. | -2或2 | D. | 0 |
3.已知2a>2b>1,则下列不等关系式中一定正确的是( )
| A. | sinα>sinb | B. | log2a<log2b | C. | a3<b3 | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
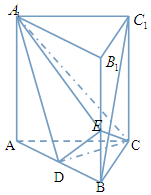 如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.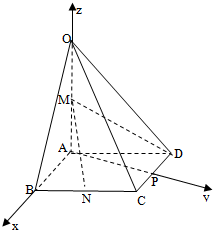 如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.
如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.