题目内容
8.下列命题中正确命题的个数是( )(1)设f(x)=ax3+bx2+cx+d(a≠0),若f(x)存在极值,则一定既有极大值又有极小值;
(2)命题“若m=3,则椭圆$\frac{x^2}{4}+\frac{y^2}{m}$=1离心率为$\frac{1}{2}$”的逆命题;
(3)设z∈C,命题“若z为实数,则z=$\overline{z}$”的否命题;
(4)设a,b∈R,命题“若ab=0,则复数z=a+bi为纯虚数”的逆否命题.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1),∵f′(x)=3ax2+2bx+c(a≠0),若f(x)存在极值,则△>0,则一定既有极大值又有极小值;
(2),若椭圆$\frac{x^2}{4}+\frac{y^2}{m}$=1离心率为$\frac{1}{2}$”,则当m>4时,$\frac{m-4}{m}=\frac{1}{4}$⇒m=$\frac{16}{3}$;
(3),设z∈C,z=a+bi(a、b为实数)“若z=$\overline{z}$“,则a+bi=a-bi⇒b=0,⇒z为实数;
(4),若b=0,复数z=a+bi为实数;
解答 解:对于(1),∵f′(x)=3ax2+2bx+c(a≠0),若f(x)存在极值,则△>0,则一定既有极大值又有极小值,故正确;
对于(2),若椭圆$\frac{x^2}{4}+\frac{y^2}{m}$=1离心率为$\frac{1}{2}$”,则当m>4时,$\frac{m-4}{m}=\frac{1}{4}$⇒m=$\frac{16}{3}$,故错;
对于(3),设z∈C,z=a+bi(a、b为实数)“若z=$\overline{z}$“,则a+bi=a-bi⇒b=0,⇒z为实数,故正确;
对于(4),若b=0,复数z=a+bi为实数,故错;
故选:B.
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.已知函数f(x)=ax2+2ax+4(-3<a<0),其图象上两点的横坐标为x1、x&2满足x1<x2,且x1+x2=1+a,则由( )
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)、f(x&2)的大小不确定 |
19.定义在R上的函数f(x),满足f(x+y)=f(x)+f(y)(x,y∈R),且f(1)=2,那么下面四个式子:
①f(1)+2f(1)+…+nf(1);
②$f[\frac{n(n+1)}{2}]$;
③n(n+1);
④n(n+1)f(1)
其中与f(1)+f(2)+…+f(n)(n∈N*)相等的是( )
①f(1)+2f(1)+…+nf(1);
②$f[\frac{n(n+1)}{2}]$;
③n(n+1);
④n(n+1)f(1)
其中与f(1)+f(2)+…+f(n)(n∈N*)相等的是( )
| A. | ①③ | B. | ①② | C. | ①②③④ | D. | ①②③ |
3.设i是虚数单位,则复数z=i(3-4i)的虚部与模的和( )
| A. | 8 | B. | 9 | C. | 5+3i | D. | 5+4i |
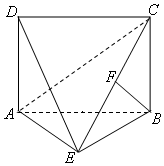 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.