题目内容
已知f(x)是定义在(0,+∞)的单调函数,且对任意的x∈(0,+∞),都有f[f(x)-lnx]=1,则函数g(x)=ex-f(x)+1的最小值必在区间( )
A、(
| ||
B、(2,
| ||
| C、(1,2) | ||
D、(
|
考点:函数最值的应用
专题:计算题,导数的综合应用
分析:利用f(x)是定义在(0,+∞)的单调函数,且对任意的x∈(0,+∞),都有f[f(x)-lnx]=1,求出f(x)=1+lnx,再求导,结合零点存在定理,即可得出结论.
解答:
解:设f(x)-lnx=m,则f(m)=1,
∴1-lnm=m,
∴m=1,
∴f(x)=1+lnx,
∴g(x)=ex-f(x)+1=ex-lnx,
∴g′(x)=ex-
,
∵g′(
)<0,g′(1)>0,
∴函数g(x)=ex-f(x)+1的最小值必在区间(
,1).
故选:D.
∴1-lnm=m,
∴m=1,
∴f(x)=1+lnx,
∴g(x)=ex-f(x)+1=ex-lnx,
∴g′(x)=ex-
| 1 |
| x |
∵g′(
| 1 |
| 2 |
∴函数g(x)=ex-f(x)+1的最小值必在区间(
| 1 |
| 2 |
故选:D.
点评:本题考查函数的最值,考查函数单调性,考查导数知识的运用,确定函数的解析式是关键.

练习册系列答案
相关题目
 某校为了解网瘾学生上网情况,抽查了100名同学,统计他们暑假期间每天平均上网时间,绘成频率分布直方图(如图).则这100名同学中每天平均上网时间在6~8小时内的同学人数为( )
某校为了解网瘾学生上网情况,抽查了100名同学,统计他们暑假期间每天平均上网时间,绘成频率分布直方图(如图).则这100名同学中每天平均上网时间在6~8小时内的同学人数为( )| A、30 | B、40 | C、50 | D、60 |
从6名教师中选4名开设A,B,C,D四门课程,每人开设一门课程且开设的课程各不相同,若这6名教师中甲、乙两人不开设A课程,则不同的选择方案共有( )
| A、300种 | B、240种 |
| C、144种 | D、96种 |
已知三棱锥的三视图如图所示,则它的体积为( )
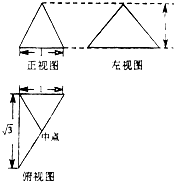

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
(
+
)10的展开式中常数项为( )
| x |
| 1 | |||
|
| A、120 | B、210 |
| C、252 | D、45 |
已知实数x,y满足条件
,则y-(
)x的最大值为( )
|
| 1 |
| 2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、1 |
如图所示的程序框图,则输出的结果为( )


| A、189 | B、381 |
| C、93 | D、45 |