题目内容
5.已知f(x)=$\frac{1}{3}{x^3}$+2xf′(1),则f′(1)等于( )| A. | 0 | B. | -1 | C. | 2 | D. | 1 |
分析 求函数的导数,让x=1,建立关于f′(1)的方程,即可求解.
解答 解:∵f(x)=$\frac{1}{3}{x^3}$+2xf′(1),
∴f′(x)=x2+2f′(1),
∴f′(1)=1+2f′(1),
∴f′(1)=-1,
故选:B.
点评 本题主要考查导数的计算和求值,利用f′(1)为常数,建立关于f′(1)的方程是解决本题的关键,比较基础.

练习册系列答案
相关题目
16.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如表:
(1)画出茎叶图;
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、方差,你认为选谁参加比赛更合适并说明理由.
| 甲 | 29 | 37 | 35 | 33 | 26 | 50 |
| 乙 | 32 | 33 | 28 | 34 | 40 | 43 |
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、方差,你认为选谁参加比赛更合适并说明理由.
10.已知集合A={1,2,3},集合B={x|x2-6x+8≤0},则A∩B=( )
| A. | {3} | B. | {2,3} | C. | {1,2,3} | D. | [2,3] |
17.集合M={x|0≤x<2},集合N={x|x2+2x-3<0},则集合M∩N=( )
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
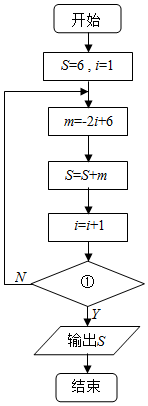 如果图中所示的流程图的输出结果为-18,那么在判断框①中用i表示的“条件”应该是i>8?.
如果图中所示的流程图的输出结果为-18,那么在判断框①中用i表示的“条件”应该是i>8?.