题目内容
3.若直线经过两点A(m,2),B(-m,2m-1)且倾斜角为45°,则m的值为( )| A. | $\frac{3}{4}$ | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
分析 由两点坐标求出直线的斜率,再由斜率等于倾斜角的正切值列式求得m的值.
解答 解:经过两点A(m,2),B(-m,2m-1)的直线的斜率为k=$\frac{2m-1-2}{-m-m}$.
又直线的倾斜角为45°,
∴$\frac{2m-1-2}{-m-m}$=tan45°=1,即m=$\frac{3}{4}$.
故选:A.
点评 本题考查直线的倾斜角,考查了直线倾斜角与斜率的关系,是基础题.

练习册系列答案
相关题目
13.集合A={x|y=ln(1-2x)},B={x|x2<x},全集U=A∪B,则∁U(A∩B)=( )
| A. | (-∞,0) | B. | $[\frac{1}{2},1]$ | C. | (-∞,0)∪$[\frac{1}{2},1]$ | D. | $(-\frac{1}{2},0]$ |
14.已知命题p:直线$x+2y-\sqrt{2}=0$与直线$x+2y-6\sqrt{2}=0$之间的距离不大于1,命题q:椭圆2x2+27y2=54与双曲线9x2-16y2=144有相同的焦点,则下列命题为真命题的是( )
| A. | p∧(¬q) | B. | (¬p)∧q | C. | (¬p)∧(¬q) | D. | p∧q |
8.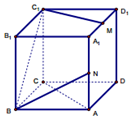 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
①C1M∥AC;
②BD1⊥AC;
③BC1与AC的所成角为60°;
④CD与BN为异面直线.
 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )①C1M∥AC;
②BD1⊥AC;
③BC1与AC的所成角为60°;
④CD与BN为异面直线.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.sin390°等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
12.设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β下面命题正确的是( )
| A. | 若l∥β,则α∥β | B. | 若α⊥β,则l⊥m | C. | 若l⊥β,则α⊥β | D. | 若α∥β,则l∥m |
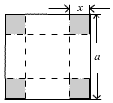 如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$.
如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$. 图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律.对捕食者和被捕食者数量之间的关系描述正确的是( )
图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律.对捕食者和被捕食者数量之间的关系描述正确的是( )


