题目内容
已知函数f（x）=x2+
．
（1）讨论函数f（x）的奇偶性（不用证明）；
（2）在区间（2，+∞）上是增函数，求a的取值范围．
| a-1 |
| x |
（1）讨论函数f（x）的奇偶性（不用证明）；
（2）在区间（2，+∞）上是增函数，求a的取值范围．
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：计算题,函数的性质及应用
分析：（1）讨论当a=1时，当a≠1，函数的奇偶性；
（2）求出导数f′（x），由于f（x）在区间（2，+∞）上是增函数，则有f′（x）≥0在（2，+∞）上恒成立．
即有a-1≤2x3，则求出右边的最小值即可．
（2）求出导数f′（x），由于f（x）在区间（2，+∞）上是增函数，则有f′（x）≥0在（2，+∞）上恒成立．
即有a-1≤2x3，则求出右边的最小值即可．
解答：
解：（1）函数f（x）=x2+
，
当a=1时，定义域为{x|x≠0}，f（x）=x2为偶函数，
当a≠1，f（x）既不是奇函数，也不是偶函数；
（2）f′（x）=2x-
，
由于f（x）在区间（2，+∞）上是增函数，
则有f′（x）≥0在（2，+∞）上恒成立．
即有a-1≤2x3，则有a-1≤24，
即有a≤17．
故a的取值范围是（-∞，17]．
| a-1 |
| x |
当a=1时，定义域为{x|x≠0}，f（x）=x2为偶函数，
当a≠1，f（x）既不是奇函数，也不是偶函数；
（2）f′（x）=2x-
| a-1 |
| x2 |
由于f（x）在区间（2，+∞）上是增函数，
则有f′（x）≥0在（2，+∞）上恒成立．
即有a-1≤2x3，则有a-1≤24，
即有a≤17．
故a的取值范围是（-∞，17]．
点评：本题考查函数的奇偶性的判断，考查函数的单调性和运用，考查运算能力，属于中档题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
已知集合A={1，2，0，-2}，B={0，2，4}，则A∩B=（ ）
| A、{1，-2} |
| B、{0，2} |
| C、{0，1，2，4，-2} |
| D、{1，-2，4} |
已知关于x的不等式
-
＞0的解集为（-∞，-2）∪（1，2），则关于x的不等式
-
＞0的解集为（ ）
| x+a |
| x+b |
| x+c |
| x+d |
| alnx-1 |
| blnx-1 |
| clnx-1 |
| dlnx-1 |
A、（-1，-
| ||||||||
B、（
| ||||||||
C、（-∞，-
| ||||||||
D、（-∞，
|
已知cos（
+α）=-
，且α为第四象限角，则cos（-3π+α）=（ ）
| 3π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
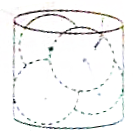如图，在底面直径为4r的圆柱内，正方放入4个半径为r的小球，使得圆柱上下表面与小球正好相切，则圆柱的高为
在正方体ABCD-A1B1C1D1中，E，F，G，H分别为CC1，C1D1，DD1，CD的中点，N为BC的中点，试在E，F，G，H四个点中找两个点，使这两个点与点N确定一个平面α，且平面α∥平面BB1D1D．