题目内容
已知x+y-3=0，求
的最小值．
| (x-2)2+(y+1)2 |
考点：函数的值域
专题：空间位置关系与距离
分析：根据题意推断出题目的几何模型，利用点到直线的距离公式求得其最小值．
解答：
解：根据题意知，本题的几何模型是直线x+y-3=0上的点到定点（2，-1）的距离，其最小值为点（2，-1）到直线的距离，即
最小值d=
=
．
最小值d=
| |2-1-3| | ||
|
| 2 |
点评：本题主要考查了两点间的距离公式，点到直线的距离公式的应用．建立几何模型是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知集合A={x|3x+x2＞0}，B={x|-4＜x＜-1}，则（ ）
| A、A∩B={x|-4＜x＜-3} |
| B、A∪B=R |
| C、B⊆A |
| D、A⊆B |
已知函数f（x）=x（lnx-
ax）有两个极值点，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、（-∞，0） | ||
B、（0，
| ||
| C、（0，1） | ||
| D、（0，+∞） |
已知“整数对”按如下规律排成一列：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），…，则第58个数对是（ ）
| A、（2，10） |
| B、（3，9） |
| C、（5，7） |
| D、（3，8） |
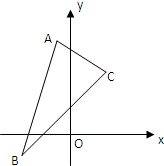已知△ABC三个顶点是A（-1，4），B（-2，-1），C（2，3）．
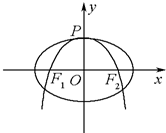如图，抛物线C：y=-