题目内容
8.如图一段程序执行后输出结果是( )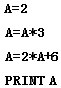
| A. | 2 | B. | 8 | C. | 18 | D. | 10 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用顺序结构计算变量A的值,并输出,逐行分析程序各语句的功能不难得到结果.
解答 解:∵A=2,
∴A=A×3=2×3=6,
∴A=2×A+6=12+6=18.
故输出的变量A的值是18.
故选:C.
点评 本题给出伪代码,求输出的A的值,着重考查了赋值语句的理解、伪代码的含义等知识,属于基础题.

练习册系列答案
相关题目
18.在等差数列{an}中,若a3+a4+a5+a6+a7=45,那么a5等于( )
| A. | 4 | B. | 5 | C. | 9 | D. | 18 |
15.某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为$\frac{3}{5}$.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
(参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d)
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3.函数f(x)=ln$\frac{3x}{2}$-$\frac{2}{x}$的零点一定位于区间( )
| A. | (0,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
17.在2×2列联表中,两个比值相差越大,两个分类变量有关系的可能性就越大,那么这两个比值为( )
| A. | $\frac{a}{a+b}$与$\frac{c}{c+d}$ | B. | $\frac{a}{c+d}$与$\frac{c}{a+b}$ | C. | $\frac{a}{a+d}$与$\frac{c}{b+c}$ | D. | $\frac{a}{b+d}$与$\frac{c}{a+c}$ |
18.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为36,焦距为12,则椭圆的方程为( )
| A. | $\frac{x^2}{36}+\frac{y^2}{64}=1$ | B. | $\frac{x^2}{100}+\frac{y^2}{64}=1$ | ||
| C. | $\frac{x^2}{36}+\frac{y^2}{64}=1或\frac{x^2}{64}+\frac{y^2}{36}=1$ | D. | $\frac{x^2}{100}+\frac{y^2}{64}=1$或$\frac{x^2}{64}+\frac{y^2}{100}=1$ |