题目内容
17.在2×2列联表中,两个比值相差越大,两个分类变量有关系的可能性就越大,那么这两个比值为( )| A. | $\frac{a}{a+b}$与$\frac{c}{c+d}$ | B. | $\frac{a}{c+d}$与$\frac{c}{a+b}$ | C. | $\frac{a}{a+d}$与$\frac{c}{b+c}$ | D. | $\frac{a}{b+d}$与$\frac{c}{a+c}$ |
分析 由题意,$\frac{a}{a+b}$-$\frac{c}{c+d}$=$\frac{ac+ad-ac-bc}{(a+b)(c+d)}$=$\frac{ad-bc}{(a+b)(c+d)}$,根据ad-bc相差越大,两个分类变量有关系的可能性就越大,即可得出结论.
解答 解:由题意,$\frac{a}{a+b}$-$\frac{c}{c+d}$=$\frac{ac+ad-ac-bc}{(a+b)(c+d)}$=$\frac{ad-bc}{(a+b)(c+d)}$,
∵ad-bc相差越大,两个分类变量有关系的可能性就越大,
∴$\frac{a}{a+b}$-$\frac{c}{c+d}$相差越大,两个分类变量有关系的可能性就越大,
故选:A.
点评 本题考查独立性检验知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
8.如图一段程序执行后输出结果是( )
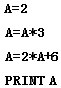
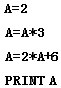
| A. | 2 | B. | 8 | C. | 18 | D. | 10 |
5.函数$y=sin(x-\frac{π}{3})$的图象的一条对称轴是( )
| A. | $x=\frac{π}{6}$ | B. | $x=-\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{3}$ |
12.盒子中有大小形状完全相同的4个红球和3个白球,从中不放回的一次摸出两个球,在第一次摸出的是红球的前提下,第二次也摸出红球的概率为( )
| A. | $\frac{2}{7}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |