题目内容
13.已知i是虚数单位,复数z满足(z-2)i=-3-i.(1)求z;
(2)若复数$\frac{x+i}{z}$在复平面内对应的点在第一象限,求实数x的取值范围.
分析 (1)利用复数的运算法则即可得出.
(2)利用复数的运算法则、几何意义、不等式的解法即可得出.
解答 解:(1)∵(z-2)i=-3-i.
∴(z-2)i•i=(-3-i)•i,化为:z-2=3i-1.
∴z=1+3i.
(2)复数$\frac{x+i}{z}$=$\frac{(x+i)(1-3i)}{(1+3i)(1-3i)}$=$\frac{x+3}{10}$+$\frac{1-3x}{10}$i在复平面内对应的点($\frac{x+3}{10}$,$\frac{1-3x}{10}$)在复在第一象限,
∴$\frac{x+3}{10}$>0且$\frac{1-3x}{10}$>0,解得$-3<x<\frac{1}{3}$.
∴实数x的取值范围是$(-3,\frac{1}{3})$.
点评 本题考查了复数的运算法则、几何意义、不等式的解法,考查推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.如图一段程序执行后输出结果是( )
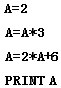
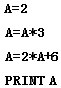
| A. | 2 | B. | 8 | C. | 18 | D. | 10 |
5.函数$y=sin(x-\frac{π}{3})$的图象的一条对称轴是( )
| A. | $x=\frac{π}{6}$ | B. | $x=-\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{3}$ |