题目内容
15.某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据在100人中随机抽取1人抽到喜欢游泳的学生的概率为$\frac{3}{5}$,可得喜爱游泳的学生,即可得到列联表;
(2)利用公式求得K2,与临界值比较,即可得到结论;
(3)利用列举法,确定基本事件的个数,即可求出概率.
解答 解:(1)因为在100人中随机抽取1人抽到喜欢游泳的学生的概率为$\frac{3}{5}$,
所以喜欢游泳的学生人数为$100×\frac{3}{5}=60$人…(1分)
其中女生有20人,则男生有40人,列联表补充如下:
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
(2)因为${K^2}=\frac{{100{{({40×30-20×10})}^2}}}{60×40×50×50}≈16.67>10.828$…(7分)
所以有99.9%的把握认为喜欢游泳与性别有关…(8分)
(3)5名学生中喜欢游泳的3名学生记为a,b,c,另外2名学生记为1,2,任取2名学生,则所有可能情况为(a,b)、(a,c)、(a,1)、(a,2)、(b,c)、(b,1)、(b,2)、(c,1)、(c,2)、(1,2),共10种…(10分)
其中恰有1人喜欢游泳的可能情况为(a,1)、(a,2)、(b,1)、(c,1)、(c,2),共6种…(11分)
所以,恰好有1人喜欢游泳的概率为$\frac{6}{10}=\frac{3}{5}$…(12分)
点评 本题考查独立性检验知识,考查概率的计算,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
5.直线y=x-4与曲线y=$\sqrt{2x}$及x轴所围成图形的面积是( )
| A. | $\frac{64}{3}$ | B. | $\frac{40}{3}$ | C. | $\frac{56}{3}$ | D. | $\frac{38}{3}$ |
10.欧阳修在《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见卖油翁的技艺之高超,若铜钱直径2百米,中间有边长为1百米的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是( )
| A. | $\frac{1}{4π}$ | B. | $\frac{1}{2π}$ | C. | $\frac{1}{π}$ | D. | $\frac{2}{π}$ |
8.如图一段程序执行后输出结果是( )
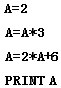
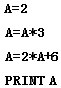
| A. | 2 | B. | 8 | C. | 18 | D. | 10 |
5.函数$y=sin(x-\frac{π}{3})$的图象的一条对称轴是( )
| A. | $x=\frac{π}{6}$ | B. | $x=-\frac{π}{6}$ | C. | $x=\frac{π}{3}$ | D. | $x=-\frac{π}{3}$ |