题目内容
 在四棱锥E-ABCD中,底面ABCD是矩形且AB=2BC=2,侧面△ADE是正三角形且垂直于底面ABCD,F是AB的中点,AD的中点为O,求:
在四棱锥E-ABCD中,底面ABCD是矩形且AB=2BC=2,侧面△ADE是正三角形且垂直于底面ABCD,F是AB的中点,AD的中点为O,求:(1)异面直线AE与CF所成的角的余弦值;
(2)点O到平面EFC的距离;
(3)二面角E-FC-D的正切值.
考点:二面角的平面角及求法,异面直线及其所成的角,点、线、面间的距离计算
专题:空间角
分析:(1)取EB的中点G,连结FG,则FG∥AE,则∠GFC为AE与CF所成角,求出CG,CF的长,即可求异面直线AE与CF所成的角的余弦值;
(2)作CF⊥ER,过O作OH⊥ER且与ER交于点H,则OH⊥平面EFC,OH的长即为点O到平面EFC的距离,利用等面积,可求点O到平面EFC的距离;
(3)由(2)知,∠ERO即为二面角E-FC-D的平面角,利用正切函数,即可求二面角E-FC-D的正切值.
(2)作CF⊥ER,过O作OH⊥ER且与ER交于点H,则OH⊥平面EFC,OH的长即为点O到平面EFC的距离,利用等面积,可求点O到平面EFC的距离;
(3)由(2)知,∠ERO即为二面角E-FC-D的平面角,利用正切函数,即可求二面角E-FC-D的正切值.
解答:
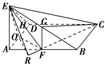 解:(1)取EB的中点G,连结FG,则FG∥AE,则∠GFC为AE与CF所成角,
解:(1)取EB的中点G,连结FG,则FG∥AE,则∠GFC为AE与CF所成角,
∵侧面△ADE是正三角形且垂直于底面ABCD,底面ABCD是矩形,
∴AB⊥平面EAD.
∴AB⊥EA?
∵AB=2BC=2,∴EB=
=
.
同理,EC=
.
∴在△EBC中,CG=
.
又∵FG=
EA=
,CF=
=
.
∴cos∠CFG=
.
∴异面直线AE与CF所成的角的余弦值为
.
(2)作CF⊥ER,则
∵侧面△ADE是正三角形,AD的中点为O,
∴EO⊥底面ABCD
∵侧面△ADE垂直于底面ABCD,
∴EO⊥底面ABCD,
∵FC?平面ABCD
∴EO⊥FC
∵EO∩ER=E
∴CF⊥平面EOR
∵CF?平面EFC
∴平面EOR⊥平面EFC.
过O作OH⊥ER且与ER交于点H,则OH⊥平面EFC,
∴OH的长即为点O到平面EFC的距离.
∵S△CFO=S矩形ABCD-S△AOF-S△CBF-S△COD?
∴OR=
.
在Rt△EOR中,OH=
=
.
∴所求距离为
.
(3)由(2)知,∠ERO即为二面角E-FC-D的平面角,
则tan∠ERO=
=
=
,
∴所求二面角的正切值为
.
 解:(1)取EB的中点G,连结FG,则FG∥AE,则∠GFC为AE与CF所成角,
解:(1)取EB的中点G,连结FG,则FG∥AE,则∠GFC为AE与CF所成角,∵侧面△ADE是正三角形且垂直于底面ABCD,底面ABCD是矩形,
∴AB⊥平面EAD.
∴AB⊥EA?
∵AB=2BC=2,∴EB=
| EA2+AB2 |
| 5 |
同理,EC=
| 5 |
∴在△EBC中,CG=
| ||
| 2 |
又∵FG=
| 1 |
| 2 |
| 1 |
| 2 |
| BC2+BF2 |
| 2 |
∴cos∠CFG=
| ||
| 4 |
∴异面直线AE与CF所成的角的余弦值为
| ||
| 4 |
(2)作CF⊥ER,则
∵侧面△ADE是正三角形,AD的中点为O,
∴EO⊥底面ABCD
∵侧面△ADE垂直于底面ABCD,
∴EO⊥底面ABCD,
∵FC?平面ABCD
∴EO⊥FC
∵EO∩ER=E
∴CF⊥平面EOR
∵CF?平面EFC
∴平面EOR⊥平面EFC.
过O作OH⊥ER且与ER交于点H,则OH⊥平面EFC,
∴OH的长即为点O到平面EFC的距离.
∵S△CFO=S矩形ABCD-S△AOF-S△CBF-S△COD?
∴OR=
3
| ||
| 4 |
在Rt△EOR中,OH=
| EO•OR |
| ER |
3
| ||
| 10 |
∴所求距离为
3
| ||
| 10 |
(3)由(2)知,∠ERO即为二面角E-FC-D的平面角,
则tan∠ERO=
| EO |
| OR |
| ||||
|
| ||
| 3 |
∴所求二面角的正切值为
| ||
| 3 |
点评:本题考查空间角,考查点到平面距离的计算,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,若函数g(x)=f(x)-k有两个不同的零点,则实数k的取值范围是( )
|
A、(
| ||
B、(0,
| ||
| C、(-∞,1) | ||
| D、(0,1) |
将直线l:y=2x按向量
=(3,0)平移得到直线l′,则l′的方程为( )
| a |
| A、y=2x-3 |
| B、y=2x+3 |
| C、y=2(x-3) |
| D、y=2(x+3) |
在边长为a的正△ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=
a,这时二面角B-AD-C的大小为( )
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
