题目内容
若对于任意的实数b∈[2，4]，都有2b（b+a）＞4恒成立，则实数a的取值范围是 ．
考点：函数恒成立问题
专题：函数的性质及应用
分析：将不等式恒成立进行转化即可求出a的取值范围．
解答：
解：对于任意的实数b∈[2，4]，都有2b（b+a）＞4恒成立，
则等价为b+a＞
，
即a＞-b+
=-b+22-b，
设f（b）=-b+22-b，则函数f（b）在b∈[2，4]上单调递减，
∴当b=2时，函数f（b）取得最大值f（2）=-2+1=-1，
则a＞-1，
故答案为：（-1，+∞）
则等价为b+a＞
| 4 |
| 2b |
即a＞-b+
| 4 |
| 2b |
设f（b）=-b+22-b，则函数f（b）在b∈[2，4]上单调递减，
∴当b=2时，函数f（b）取得最大值f（2）=-2+1=-1，
则a＞-1，
故答案为：（-1，+∞）
点评：本题主要考查不等式恒成立的求解，利用参数分离法，转化为求函数的最值是解决本题的关键．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
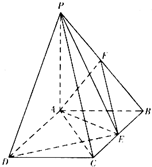如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=