题目内容
2.某跨国饮料公司对全世界所有人均GDP(即人均纯收入)在0.5-8千美元的地区销售,该公司在对M饮料的销售情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.(1)下列几个模拟函数中(x表示人均GDP,单位:千美元;y表示年人均M饮料的销量,单位:升),用哪个来描述人均饮料销量与地区的人均GDP的关系更合适?说明理由;
(A)f(x)=ax2+bx
(B)f(x)=logax+b
(C)f(x)=ax+b
(2)若人均GDP为2千美元时,年人均M饮料的销量为6升;人均GDP为4千美元时,年人均M饮料的销量为8升;把你所选的模拟函数求出来;
(3)因为M饮料在N国被检测出杀虫剂的含量超标,受此事件影响,M饮料在人均GDP不高于3千美元的地区销量下降5%,不低于5千美元的地区销量下降5%,其他地区的销量下降10%,根据(2)所求出的模拟函数,求在0.5-8千美元的地区中,年人均M饮料的销量最多为多少?
分析 (1)考虑到A,B,C,D四个函数中只有A符合题意,因为B,C,D三个函数是单调函数.
(2)用待定系数法求出A的解析式可得.
(3)根据题中人均GDP的要求范围把x的取值分成三段,分别求出每一段的最大值,并比较去最大即可.
解答 解:(1)由于(B)、(C)、(D)三个函数,在[0.5,8]上均为单调函数,…(2分)
而(A)为二次函数,不单调,故(A)更适合…(4分)
(2)由题意$\left\{\begin{array}{l}f(2)=6\\ f(4)=8\end{array}\right.⇒$a=-$\frac{1}{2}$,b=4…(6分)
则$f(x)=-\frac{1}{2}{x^2}+4x$,x∈[0.5,8]…(8分)
(3)设受事件影响后,各地区M饮料销售量为g(x),则$g(x)=\left\{\begin{array}{l}\frac{19}{20}(-\frac{1}{2}{x^2}+4x),\;\;0.5≤x≤3\\ \frac{9}{10}(-\frac{1}{2}{x^2}+4x),\;\;3<x<5\\ \frac{19}{20}(-\frac{1}{2}{x^2}+4x),\;\;5≤x≤8\end{array}\right.$
当x∈[0.5,3]时,y=$\frac{19}{20}$[-$\frac{1}{2}$(x-4)2+8],在x∈[0.5,3]上递增,所以ymax=$\frac{57}{8}$
当x∈[5,8]时,y=$\frac{19}{20}$[-$\frac{1}{2}$(x-4)2+8],在x∈[5,8]上递减,所以ymax=$\frac{57}{8}$
当x∈(3,5)时,y=$\frac{9}{10}$[-$\frac{1}{2}$(x-4)2+8],4∈(3,5),所以ymax=$\frac{36}{5}$
比较大小得:当x=4时,ymax=$\frac{36}{5}$
答:当人均GDP在4千美元的地区,人均A饮料的销量最多为$\frac{36}{5}$.
点评 考查学生会根据实际问题选择函数类型,会用不同的自变量取值求二次函数的最值及比较出最值.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | ?x0∈z,1<4x0<3 | B. | ?x0∈z,4x0+1=0 | C. | ?x∈R,x2-1=0 | D. | ?x∈R,x2-2x+2≥0 |
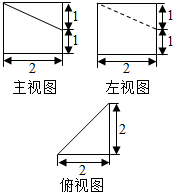
| A. | $\frac{23}{3}$ | B. | 4$\sqrt{2}$+$\sqrt{6}$+6 | C. | 6$\sqrt{2}$+6 | D. | 4$\sqrt{2}$+$\sqrt{6}$+8 |