题目内容
13.已知函数f(x)=lg(x+1)(1)当x∈[1,9]时,求函数f(x)的反函数;
(2)若0<f(1-2x)-f(x)<1,求x的取值范围.
分析 (1)先确定函数的值域,就是其反函数的定义域,再对函数求反函数;
(2)将该不等式等价为:1<$\frac{2-2x}{x+1}$<10且x+1>0,再直接解不等式即可.
解答 解:(1)∵y=f(x)=lg(x+1),
∴当x∈[1,9]时,y∈[lg2,1],
且x+1=10y,即x=10y-1,
互换x,y得,y=10x-1,
所以,f-1(x)=10x-1,x∈[lg2,1];
(2)不等式0<f(1-2x)-f(x)<1可化为:
0<lg$\frac{2-2x}{x+1}$<1,等价为:
1<$\frac{2-2x}{x+1}$<10且x+1>0,
解得x∈(-$\frac{2}{3}$,$\frac{1}{3}$),
所以,原不等式中x的取值范围为:(-$\frac{2}{3}$,$\frac{1}{3}$).
点评 本题主要考查了反函数的解法及其定义域的确定,以及对数不等式与分式不等式的解法,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
5.已知函数f(x)=2loga(x-1)(a>0且a≠1)恒过点(m,n),则在直角坐标系中,函数$g(x)={(\frac{1}{m+n})^{|{x+1}|}}$的大致图象为( )
| A. | 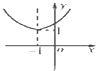 | B. | 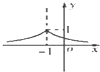 | C. | 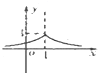 | D. | 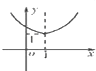 |
6.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(x,-2),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则向量$\overrightarrow{a}$-$\overrightarrow{b}$的模为( )
| A. | 5 | B. | $2\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{2}$ |
18.若2014=αk•5k+αk-1•5k-1+…+a1•51+a0•50,其中ak,ak-1,…,a0∈N,0<ak<5,0≤ak-1,ak-2,…,a1,a0<5.现从a0,a1,…,ak中随机取两个数分别作为点P的横、纵坐标,则点P落在椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1内的概率是( )
| A. | $\frac{11}{25}$ | B. | $\frac{13}{25}$ | C. | $\frac{17}{25}$ | D. | $\frac{11}{16}$ |
4.已知f(x)是偶函数,且在[0,1]上是增函数,则f(0.5)、f(-1)、f(0)的大小关系是( )
| A. | f(0.5)<f(0)<f(-1) | B. | f(-1)<f(0.5)<f(0) | C. | f(0)<f(0.5)<f(-1) | D. | f(-1)<f(0)<f(0.5) |