题目内容
10.已知:函数f(x)=ax2-bx+c,若f(x)的顶点坐标为(1,2),且f(0)=3,(1)求a,b,c的值
(2)若x∈[-1,2],求函数f(x)值域.
分析 (1)由已知可得$\left\{\begin{array}{l}\begin{array}{c}-\frac{b}{2a}=1\\ f(1)=2\\ f(0)=3\end{array}\right.\end{array}\right.$,即$\left\{\begin{array}{l}b=-2a\\ a-b+c=2\\ c=3\end{array}\right.$,解得a,b,c的值
(2)分析x∈[-1,2]时函数的图象和性质,求出最值,进而可得函数的值域.
解答 解:(1)∵f(x)的顶点坐标为(1,2),且f(0)=3,
∴$\left\{\begin{array}{l}\begin{array}{c}-\frac{b}{2a}=1\\ f(1)=2\\ f(0)=3\end{array}\right.\end{array}\right.$,即$\left\{\begin{array}{l}b=-2a\\ a-b+c=2\\ c=3\end{array}\right.$…(3分)
解得 a=1,b=2,c=3 …(6分)
(2)函数f(x)=x2-2x+3的对称轴为x=1…(8分),
x∈[-1,2]时,fmin(x)=f(1)=2…(10分)
fmax(x)=f(-1)=6…(12分)
∴x∈[-1,2]时,值域为[2,6]…(14分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某程序框图如图所示,则该程序运行后输出的k的值是( )

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.下列关系式中表述正确的是( )
| A. | 0∈{(0,0)} | B. | 0∈∅ | C. | 0∈N | D. | {0}∈{x|x2=0} |
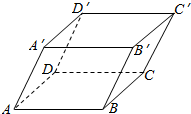 如图,已知平行六面体ABCD-A′B′C′D′,化简下列各表达式,并在图中标出化简结果的向量:
如图,已知平行六面体ABCD-A′B′C′D′,化简下列各表达式,并在图中标出化简结果的向量: