题目内容
9.某几何体的三视图如图所示,则该几何体的表面积( )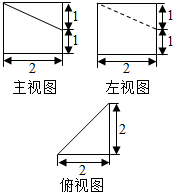
| A. | $\frac{23}{3}$ | B. | 4$\sqrt{2}$+$\sqrt{6}$+6 | C. | 6$\sqrt{2}$+6 | D. | 4$\sqrt{2}$+$\sqrt{6}$+8 |
分析 根据三视图得出该几何体在边长为2的正方体内部,画出几何图形,利用表面积公式求出各个面的面积即可.
解答  解:根据几何体的三视图,得:
解:根据几何体的三视图,得:
该几何体是如图所示的多面体ABCDEF,
则S直角梯形ABFE=S直角梯形BCDF=$\frac{1}{2}$×(1+2)×2=3,
S△ABC=$\frac{1}{2}$×2×2=2,S矩形ACDE=2$\sqrt{2}$×2=4$\sqrt{2}$,
S△DEF=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{{(\sqrt{5})}^{2}{-(\sqrt{2})}^{2}}$=$\sqrt{6}$;
所以该几何体的表面积是S=2×3+2+4$\sqrt{2}$+$\sqrt{6}$=4$\sqrt{2}$+$\sqrt{6}$+8.
故选:D.
点评 本题考查了利用三视图求空间几何体的表面积的应用问题,也考查了空间想象能力和逻辑思维能力的应用问题,是易错题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若某几何体的三视图如图所示,则该几何体的表面积为( )
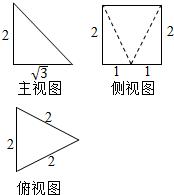

| A. | 4+$\sqrt{7}$ | B. | 8+$\sqrt{7}$ | C. | 4+$\sqrt{3}$+$\sqrt{7}$ | D. | 8+$\sqrt{3}$+$\sqrt{7}$ |
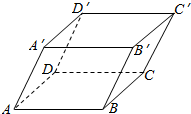 如图,已知平行六面体ABCD-A′B′C′D′,化简下列各表达式,并在图中标出化简结果的向量:
如图,已知平行六面体ABCD-A′B′C′D′,化简下列各表达式,并在图中标出化简结果的向量: