题目内容
(本小题满分12分)已知函数 在同一半周期内的图象过点
在同一半周期内的图象过点 ,其中
,其中 为坐标原点,
为坐标原点, 为函数
为函数 图象的最高点,
图象的最高点, 为函数
为函数 的图象与
的图象与 轴的正半轴的交点.
轴的正半轴的交点.

(Ⅰ)求证: 为等腰直角三角形.
为等腰直角三角形.
(Ⅱ)将 绕原点
绕原点 按逆时针方向旋转角
按逆时针方向旋转角 ,得到
,得到 ,若点
,若点 恰好落在曲线
恰好落在曲线
 上(如图所示),试判断点
上(如图所示),试判断点 是否也落在曲线
是否也落在曲线
 上,并说明理由.
上,并说明理由.
(Ⅰ)详见解析; (Ⅱ)点 不落在曲线
不落在曲线
 上.
上.
【解析】
试题分析:(Ⅰ)因为函数 的最小正周期
的最小正周期 ,所以函数
,所以函数 的半周期为4,故
的半周期为4,故 . 又因为
. 又因为 为函数
为函数 图象的最高点,所以点
图象的最高点,所以点 坐标为
坐标为 ,故
,故 ,又因为
,又因为 坐标为
坐标为 ,所以
,所以 ,根据勾股定理,即可证明
,根据勾股定理,即可证明 为等腰直角三角形. (Ⅱ)
为等腰直角三角形. (Ⅱ)
由(Ⅰ)知, ,
, 所以点
所以点 ,
, 的坐标分别为
的坐标分别为 ,
,
 , 因为点
, 因为点 在曲线
在曲线
 上,所
上,所 ,根据角的范围,化简可得
,根据角的范围,化简可得 ,所以点
,所以点 不落在曲线
不落在曲线
 上.
上.
试题解析:【解析】
(Ⅰ)因为函数 的最小正周期
的最小正周期 , 1分
, 1分
所以函数 的半周期为4,
的半周期为4,
故 . 2分
. 2分
又因为 为函数
为函数 图象的最高点,
图象的最高点,
所以点 坐标为
坐标为 ,故
,故 , 3分
, 3分
又因为 坐标为
坐标为 ,所以
,所以 ,
,
所以 且
且 ,所以
,所以 为等腰直角三角形. 5分
为等腰直角三角形. 5分
(Ⅱ)点 不落在曲线
不落在曲线
 上. 6分
上. 6分
理由如下:
由(Ⅰ)知, ,
,
所以点 ,
, 的坐标分别为
的坐标分别为 ,
, , 8分
, 8分
因为点 在曲线
在曲线
 上,
上,
所以 ,
,
即 ,又
,又 ,所以
,所以 . 10分
. 10分
又 .
.
所以点 不落在曲线
不落在曲线
 上. 12分
上. 12分
考点:1.三角函数的图象与性质、三角函数的定义;2.二倍角公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的定义域是( )
的定义域是( ) B.
B.  C.
C.  D.
D. 
 上.用一平行于平面
上.用一平行于平面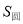 和
和 ,那么
,那么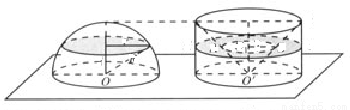
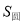
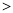
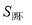 B.
B.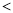
 的边长为
的边长为 ,
, 为
为 的中点,
的中点,  为
为 的中点,则
的中点,则 _______.
_______. 0.5
0.5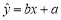 .若
.若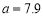 ,则
,则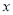 每增加1个单位,
每增加1个单位,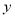 就
就 个单位 B.减少
个单位 B.减少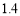 个单位
个单位  个单位 D.减少
个单位 D.减少 个单位
个单位  是某三角形的三个内角,给出下列四组数据:
是某三角形的三个内角,给出下列四组数据: ; ②
; ② ;
; ; ④
; ④ .
. 的左焦点为
的左焦点为 ,点
,点 是椭圆上异于顶点的任意一点,
是椭圆上异于顶点的任意一点, 为坐标原点.若点
为坐标原点.若点 是线段
是线段 的中点,则
的中点,则 的周长为( ).
的周长为( ). B.
B. C.
C. D.
D.
 ,则
,则 中的所有偶数的和等于 .
中的所有偶数的和等于 . 中,
中,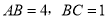
 为
为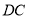 的四等分点(靠近
的四等分点(靠近 处),
处), 为线段
为线段 上一动点(包括端点),现将
上一动点(包括端点),现将 沿
沿 折起,使
折起,使 点在平面内的射影恰好落在边
点在平面内的射影恰好落在边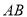 上,则当
上,则当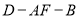 的平面角余弦值的变化范围为 .
的平面角余弦值的变化范围为 .