题目内容
9.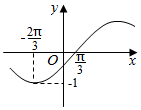 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图:
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图:(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若将函数f(x)图象上的所有点的纵坐标保持不变,横坐标缩小到原来的$\frac{1}{4}$倍,再沿x轴向左平移$\frac{π}{4}$个单位长度,得到函数g(x)的图象,求函数g(x)在[-$\frac{π}{4}$,$\frac{π}{6}$]上的值域.
分析 (1)根据函数图象确定A,ω和φ的值即可.
(2)根据三角函数平移关系,结合三角函数的单调性进行求解即可.
解答 解:(Ⅰ)由图象知A=1,函数的周期T=4•[$\frac{π}{3}$-(-$\frac{2π}{3}$)]=4π,
即$\frac{2π}{ω}$=4π,则ω=$\frac{1}{2}$,
∵函数图象与x的交点坐标是($\frac{π}{3}$,0),
∴Asin($\frac{1}{2}$×$\frac{π}{3}$+φ)=0
即sin($\frac{π}{6}$+φ)=0
即$\frac{π}{6}$+φ=kπ,即φ=kπ-$\frac{π}{6}$,
∵|φ|<$\frac{π}{2}$,
∴当k=0时,φ=-$\frac{π}{6}$,
即f(x)=sin($\frac{1}{2}$x-$\frac{π}{6}$),
则f(x)=sin($\frac{1}{2}$x-$\frac{π}{6}$).
(Ⅱ)若将函数f(x)图象上的所有点的纵坐标保持不变,横坐标缩小到原来的$\frac{1}{4}$倍,得到y=sin(2x-$\frac{π}{6}$),
再沿x轴向左平移$\frac{π}{4}$个单位长度,得到函数g(x)的图象,
即g(x)=sin[2(x+$\frac{π}{4}$)-$\frac{π}{6}$]=sin(2x+$\frac{π}{3}$),
∵x∈[-$\frac{π}{4}$,$\frac{π}{6}$],
∴2x+$\frac{π}{3}$∈[-$\frac{π}{6}$,$\frac{2π}{3}$],
则当2x+$\frac{π}{3}$=$\frac{π}{2}$时,函数取得最大值2,
当2x+$\frac{π}{3}$=-$\frac{π}{6}$时,函数取得最小值-1,
即函数g(x)在[-$\frac{π}{4}$,$\frac{π}{6}$]上的值域是[-1,2].
点评 本题主要考查三角函数解析式的求解以及三角函数单调性的应用,考查学生的运算和推理能力.根据条件求出函数的解析式是解决本题的关键.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案| A. | 2${A}_{4}^{4}$ | B. | ${A}_{4}^{4}$•${A}_{3}^{3}$ | C. | ${A}_{4}^{4}$•${A}_{4}^{4}$ | D. | ${A}_{8}^{8}$ |