题目内容
14.已知函数f(x)=(x2-a+1)ex(a∈R)有两个不同的极值点m,n,(m<n),且|m+n|+1≥|mn|.(1)求实数a的取值范围;
(2)当x∈[0,2]时,设函数y=mf(x)的最大值为g(m),求g(m).
分析 (1)由f(x)得到其导函数,由两个极值点,得知导函数有2个根,且由韦达定理知两个之和与两根之积.
(2)求出m的范围,化简y,根据导数求出g(m)的最大值.
解答 解:(1)函数f(x)=(x2-a+1)ex.
∴f′(x)=(x2+2x-a+1)ex.
令f′(x)=0,得:x2+2x-a+1=0.
由题意:△=4-4(1-a)=4a>0.
即a>0,
且:m+n=-2,mn=1-a.
∵|m+n|+1≥|mn|.
∴|a-1|≤3.
∴0<a≤4.
(2)∵f′(m)=(m2+2m-a+1)em=0.
∴a=m2+2m+1.
∴0<m2+2m+1≤4.
∴-3≤m≤1且m≠-1.
又∵m<n.
∴-3≤m<-1.
∴y=mf(x).
∴g(m)=m(m2-a+1)em=m(m2-m2-2m)em=-2m2em.
g′(m)=-2m(2+m)em .
令g′(x)=0,得m1=0,m2=-2.
∴g(m)在[0,2]上是单调递减.
g(m)最大值为g(0)=0.
点评 本题考查利用导数研究函数在闭区间上的最值,一般是求导函数对应方程的根,然后求出根对应的函数值,根据单调性,得到最值.

练习册系列答案
相关题目
5.已知x与y之间的一组数据:则y与x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
| A. | (1,2) | B. | (5,2) | C. | (2,5) | D. | (2.5,5) |
6.设复数z=2+i,则复数z(1-z)的共轭复数为( )
| A. | -1-3i | B. | -1+3i | C. | 1+3i | D. | 1-3i |
3.设全集U=R,集合A={x|-4<x<1},B={x|4${\;}^{x+\frac{1}{2}}$>$\frac{1}{8}$},则图中阴影部分所表示的集合为( )
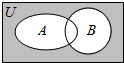

| A. | (-2,1] | B. | (1,+∞) | C. | (-∞,-4] | D. | (-∞,-4]∪(-2,1) |
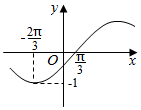 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图:
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图: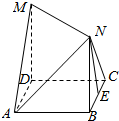 如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD且MD=NB=1,E为BC的中点