题目内容
18.函数f(x)=$\left\{\begin{array}{l}{|lnx-2|,}&{x>0}\\{-{x}^{2}-2x+3,}&{x≤0}\end{array}\right.$,直线y=m与函数f(x)的图象交于四个不同的点,交点横坐标从小到大依次记为a,b,c,d,下列说法正确的是②③.(请写出所有正确答案的序号)①m∈(3,4);
②abcd∈[0,e4);
③a+b+c+d∈[e5+$\frac{1}{e}$-2,e6+$\frac{1}{{e}^{2}}$-2);
④若关于x的方程f(x)+x=t恰有三个不同实根,则t=3.
分析 ①画出y=f(x)与y=m的图象即可;
②,结合图象把abcd的不等式用m表示出来;
③同样用m把a+b+c+d表示出来;
④若关于x的方程f(x)+x=t恰有三个不同实根,则y=f(x)与y=-x+t有三个不同的交点,画图即可.
解答  解:∵函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x+3,x≤0}\\{|2-lnx|,x>0}\end{array}\right.$,即f(x)=$\left\{\begin{array}{l}{-(x+1)^{2}+4,x≤0}\\{|2-lnx|,x>0}\end{array}\right.$,
解:∵函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x+3,x≤0}\\{|2-lnx|,x>0}\end{array}\right.$,即f(x)=$\left\{\begin{array}{l}{-(x+1)^{2}+4,x≤0}\\{|2-lnx|,x>0}\end{array}\right.$,
∴函数f(x)的图象如下:
若直线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈[3,4),故①错误;
四个交点横坐标从小到大,依次记为a,b,c,d,则a,b关于x=-1对称,
∴a+b=-2,ab=m-3,∴ab∈[0,1),且lnc=2-m,lnd=2+m,
∴ln(cd)=4,
∴cd=e4,
∴abcd∈[0,e4),∴②是正确的;
由2-lnx=4得x=$\frac{1}{{e}^{2}}$,由2-lnx=3得x=$\frac{1}{e}$,
∴c∈($\frac{1}{{e}^{2}}$,$\frac{1}{e}$],又∵cd=e4,
∴a+b+c+d=c+$\frac{{e}^{4}}{c}$-2在($\frac{1}{{e}^{2}}$,$\frac{1}{e}$]是递减函数,∴a+b+c+d∈[e5+$\frac{1}{e}$-2,e6+$\frac{1}{{e}^{2}}$-2);
∴③是正确的;
④若关于x的方程f(x)+x=t恰有三个不同实根,则y=f(x)与y=-x+t有三个不同的交点,
而直线y=-x+3 与y=-x+$\frac{13}{4}$均与y=f(x)有三个交点,∴t不唯一.∴故④错误,
故正确的是②③,
故答案为:②③
点评 本题主要考查与函数有关的命题的真假判断,利用数形结合以及分段函数的性质是解决本题的关键.综合性较强,难度较大.

 培优口算题卡系列答案
培优口算题卡系列答案| A. | -1-3i | B. | -1+3i | C. | 1+3i | D. | 1-3i |
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
| A. | (-2,1] | B. | (1,+∞) | C. | (-∞,-4] | D. | (-∞,-4]∪(-2,1) |
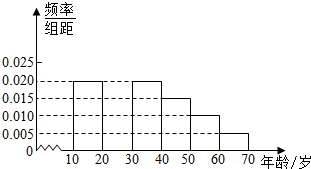 某社区为调查当前居民的睡眠状况,从该社区的[10,70]岁的人群中随机抽取n人进行一次日平均睡眠时间调查,这n人中各年龄组人数的频率分布直方图如图1所示,统计各年龄组的“亚健康族”(日平均睡眠时间符合健康标准的称为“健康族”否则称为“亚健康族”)人数及相应频率,得到统计表如图所示
某社区为调查当前居民的睡眠状况,从该社区的[10,70]岁的人群中随机抽取n人进行一次日平均睡眠时间调查,这n人中各年龄组人数的频率分布直方图如图1所示,统计各年龄组的“亚健康族”(日平均睡眠时间符合健康标准的称为“健康族”否则称为“亚健康族”)人数及相应频率,得到统计表如图所示 | 组数 | 分组 | 亚健康族的人数 | 占本组的频率 |
| 第一组 | [10,20) | 100 | 0.5 |
| 第二组 | [20,30) | 195 | P |
| 第三组 | [30,40) | 120 | 0.6 |
| 第四组 | [40,50) | a | 0.4 |
| 第五组 | [50,60) | 30 | 0.3 |
| 第六组 | [60,70] | 15 | 0.3 |
(2)用分层抽样的方法从年龄在[30,50)岁的“亚健康族”中抽取6人参加健康睡眠体验活动,现从6人中随机选取2人担任领队,记年龄在[40,50)岁的领队有X人,求X的分布列及数学期望.
| A. | $\frac{π}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{2}{3}$ |
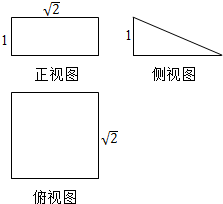 一个几何体的三视图及其尺寸(单位:cm)如图所示.
一个几何体的三视图及其尺寸(单位:cm)如图所示.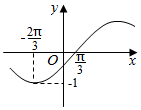 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图:
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图: