题目内容
17.设函数f(x)=4x2-lnx,且f′(m)=0,则m=$\frac{\sqrt{2}}{4}$.分析 求函数的导数,解导数方程即可.
解答 解:函数的导数为f′(x)=8x-$\frac{1}{x}$,
则由f′(m)=0得8m-$\frac{1}{m}$=0,得8m2=1,得m=±$\frac{\sqrt{2}}{4}$,
∵函数的定义域为(0,+∞),
∴m>0,则m=$\frac{\sqrt{2}}{4}$,
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题主要考查导数的计算,要求熟练掌握掌握常见函数的导数公式,比较基础.

练习册系列答案
相关题目
7.若命题p:?x∈R,x2-3x+5>0,则该命题的否定是( )
| A. | ?x∈R,x2-3x+5≤0 | B. | ?x∈R,x2-3x+5>0 | C. | ?x∈R,x2-3x+5<0 | D. | ?x∈R,x2-3x+5≤0 |
5.已知x与y之间的一组数据:则y与x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点( )
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
| A. | (1,2) | B. | (5,2) | C. | (2,5) | D. | (2.5,5) |
6.设复数z=2+i,则复数z(1-z)的共轭复数为( )
| A. | -1-3i | B. | -1+3i | C. | 1+3i | D. | 1-3i |
7.曲线y=$\sqrt{x}$在[0,1]上围绕x轴旋转一周,形成的几何体体积为( )
| A. | $\frac{π}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{2}{3}$ |
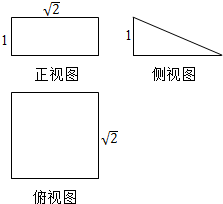 一个几何体的三视图及其尺寸(单位:cm)如图所示.
一个几何体的三视图及其尺寸(单位:cm)如图所示.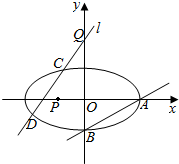 已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.
已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$ (a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(a,0)和B(0,-b)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.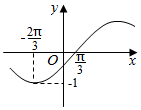 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图:
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图: