题目内容
12.化简$\frac{sin(α+π)cos(π-α)sin(\frac{5}{2}π-α)}{tan(-α)co{s}^{2}(-α-2π)}$=-cosα.分析 由诱导公式和同角三角函数基本关系逐步化简可得.
解答 解:由诱导公式和同角三角函数基本关系化简可得:
$\frac{sin(α+π)cos(π-α)sin(\frac{5}{2}π-α)}{tan(-α)co{s}^{2}(-α-2π)}$
=$\frac{(-sinα)(-cosα)cosα}{-\frac{sinα}{cosα}•co{s}^{2}α}$
=-cosα,
故答案为:-cosα.
点评 本题考查三角函数化简,涉及诱导公式和同角三角函数基本关系,属基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
20.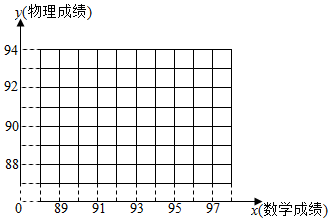 某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
(1)请在下图的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
(2)要从4名语文成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的英语成绩高于90分的人数,求随机变量X不小于1的概率.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
 某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 语文(x分) | 89 | 91 | 93 | 95 | 97 |
| 英语(y分) | 87 | 89 | 89 | 92 | 93 |
(2)要从4名语文成绩在90分以上的同学中选2人参加一项活动,以X表示选中的同学的英语成绩高于90分的人数,求随机变量X不小于1的概率.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
17.设p:?x∈R,x2-4x+3m>0,q:f(x)=x3+2x2+mx+1在(-∞,+∞)内单调递增,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.为了了解某天甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,
测量产品中的微量元素x,y的含量(单位:微克),当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.已知该天甲厂生产的产品共有98件,如表是乙厂的5件产品的测量数据:
(1)求乙厂该天生产的产品数量;
(2)用上述样本数据统计乙厂该天生产的优等品的数量;
(3)从乙厂抽取的上述5件产品中,随机抽取2件.求抽取的2件产品中优等品的件数X的分布列及数学期望.
测量产品中的微量元素x,y的含量(单位:微克),当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.已知该天甲厂生产的产品共有98件,如表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(2)用上述样本数据统计乙厂该天生产的优等品的数量;
(3)从乙厂抽取的上述5件产品中,随机抽取2件.求抽取的2件产品中优等品的件数X的分布列及数学期望.