题目内容
2．由x=0，y=x3，y=1所围成的平面图形绕y轴旋转一周，所得几何体体积是$\frac{3π}{5}$．分析 利用求旋转体的体积公式，对其求积分，求得体积V=$\frac{3π}{5}$．
解答 解：旋转体所得到的体积公式得：$V={π∫}_{0}^{1}（\root{3}{y}）^{2}dy$
解得V=$\frac{3}{5}π$
故答案为：$\frac{3π}{5}$．
点评 本题主要考察旋转体的体积公式，求积分，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
13．已知l，m，n为三条不同直线，α，β，γ为三个不同平面，则下列判断正确的是（ ）
| A． | 若m∥α，n∥α，则m∥n | B． | 若m⊥α，n∥β，α⊥β，则m⊥n | ||
| C． | 若α∩β=l，m∥α，m∥β，则m∥l | D． | 若α∩β=m，α∩γ=n，l⊥m，l⊥n，则l⊥α |
10．过点（3，1）作圆（x-2）2+（y-2）2=4的弦，其中最短的弦长为（ ）
| A． | $\sqrt{2}$ | B． | $2\sqrt{2}$ | C． | 3 | D． | 4 |
17．从某山区养殖场散养的3500头猪中随机抽取5头，测量猪的体长x（cm）和体重y（kg），得如下测量数据：
（1）当且仅当x，y满足：x≥180且y≥100时，该猪为优等品，用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量；
（2）从抽取的上述5头猪中，随机抽取2头中优等品数x的分布列及其数学期望．
| 猪编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 181 | 166 | 185 | 180 |
| y | 95 | 100 | 97 | 103 | 101 |
（2）从抽取的上述5头猪中，随机抽取2头中优等品数x的分布列及其数学期望．
7．
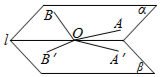如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（ ）
如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（ ）| A． | ∠A′OB′为钝角 | B． | ∠A′OB′＞∠AOB | ||
| C． | ∠AOB+∠AOA′＜π | D． | ∠B′OB+∠BOA+∠AOA′＞π |
已知F1、F2是椭圆C的左右焦点，点A，B为其左右顶点，P为椭圆C上（异于A、B）的一动点，当P点坐标为（1，$\frac{3}{2}$）时，△PF1F2的面积为$\frac{3}{2}$，分别过点A、B、P作椭圆C的切线l1，l2，l，直线l与l1，l2分别交于点R，T．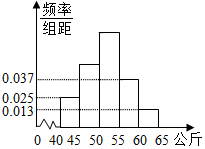
人的体重是人的身体素质的重要指标之一．某校抽取了高二的部分学生，测出他们的体重（公斤），体重在40公斤至65公斤之间，按体重进行如下分组：第1组[40，45），第2组[45，50），第3组[50，55），第4组[55，60），第5组[60，65]，并制成如图所示的频率分布直方图，已知第1组与第3组的频率之比为1：3，第3组的频数为90．