题目内容
1．为了了解某天甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件，测量产品中的微量元素x，y的含量（单位：微克），当产品中的微量元素x，y满足x≥175，且y≥75时，该产品为优等品．已知该天甲厂生产的产品共有98件，如表是乙厂的5件产品的测量数据：
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
（2）用上述样本数据统计乙厂该天生产的优等品的数量；
（3）从乙厂抽取的上述5件产品中，随机抽取2件．求抽取的2件产品中优等品的件数X的分布列及数学期望．
分析 （1）由题意，利用频率=$\frac{频数}{总数}$，能求出乙厂生产的产品总数．
（2）由题意，先求出样品中优等品的概率，由此能求出乙厂生产的优等品数量．
（3）由表可得X的可能取值为0，1，2，分别求出相应的概率，由此能求出X的分布列为和数学期望．
解答 解：（1）由题意，乙厂生产的产品总数为5÷$\frac{14}{98}$=35．
（2）样品中优等品的概率为$\frac{2}{5}$，乙厂生产的优等品数量为35×$\frac{2}{5}=14$．
（3）由表可得X的可能取值为0，1，2，
P（X=0）=$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{3}{10}$，
P（X=1）=$\frac{{C}_{3}^{1}{C}_{2}^{1}}{{C}_{5}^{2}}$=$\frac{3}{5}$，
P（X=2）=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{10}$，
∴X的分布列为：
| X | 0 | 1 | 3 |
| P | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
点评 本题考查分层抽样、频率分布列的应用，考查离散型随机变量的分布列、数学期望的求法，是中档题，解题时要认真审题，注意排列组合知识的合理运用．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
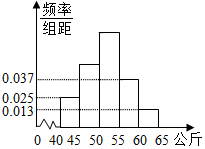人的体重是人的身体素质的重要指标之一．某校抽取了高二的部分学生，测出他们的体重（公斤），体重在40公斤至65公斤之间，按体重进行如下分组：第1组[40，45），第2组[45，50），第3组[50，55），第4组[55，60），第5组[60，65]，并制成如图所示的频率分布直方图，已知第1组与第3组的频率之比为1：3，第3组的频数为90．
6．已知点P是函数y=sin（2x+α）图象与x轴的一个交点，A，B为P点右侧距离点P最近的一个最高点和最低点，则$\overrightarrow{PA}$•$\overrightarrow{PB}$=（ ）
| A． | $\frac{{π}^{2}}{4}$-1 | B． | $\frac{3{π}^{2}}{16}$-1 | C． | $\frac{3{π}^{2}}{4}$-1 | D． | $\frac{{π}^{2}}{8}$-1 |