题目内容
由200名学生的某次数学考试成绩绘制成了频率分布直方图(如图).由图可知在该次数学考试中成绩小于60分的学生数是( )


| A、600 | B、60 | C、40 | D、4 |
考点:频率分布直方图
专题:图表型,概率与统计
分析:根据频率=小矩形的面积=小矩形的高×组距.求出成绩小于60分的频率,再根据频数=样本容量×频率计算可得答案.
解答:
解:由频率分布直方图知:数学考试中成绩小于60分的是从左数前三组,
其频率为0.002×10+0.006×10+0.012×10=0.2,
∴成绩小于60分的学生数为200×0.2=40人.
故选:C.
其频率为0.002×10+0.006×10+0.012×10=0.2,
∴成绩小于60分的学生数为200×0.2=40人.
故选:C.
点评:本题考查频率分布直方图,在频率分布直方图中频率=
=小矩形的面积=小矩形的高×组距.
| 频数 |
| 样本容量 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中的真命题是( )
| A、若m∥α,n∥β,α∥β,则m∥n |
| B、若m∥α,n∥β,α⊥β,则m⊥n |
| C、若m⊥α,n⊥β,α⊥β,则m∥n |
| D、若m⊥α,n∥β,α∥β,则m⊥n |
设等比数列{an}的前n项和为Sn,若Sm-1=5,Sm=-11,Sm+1=21,则m=( )
| A、3 | B、4 | C、5 | D、6 |
已知x,y满足约束条件
,则z=x+3y的最小值为( )
|
| A、1 | B、2 | C、3 | D、4 |
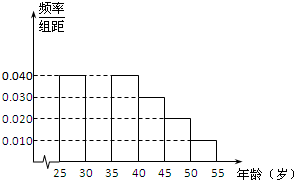 某班研究性学习小组在今年11月11日“双11购物节”期间,对[25,55)岁的人群随机抽取了1000人进行了一次是否参加“抢购商品”的调查,得到如下统计表和各年龄段人数频率分布直方图.
某班研究性学习小组在今年11月11日“双11购物节”期间,对[25,55)岁的人群随机抽取了1000人进行了一次是否参加“抢购商品”的调查,得到如下统计表和各年龄段人数频率分布直方图. 