题目内容
下列命题中,真命题是( )
| A、?x0∈R,ex0≤0 | ||||
| B、?x∈R,2x>x2 | ||||
C、双曲线x2-y2=1的离心率为
| ||||
D、双曲线x2-
|
考点:命题的真假判断与应用
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:A.由指数函数的性质可得?x∈R,则ex>0,即可判断出;
B.取x=2,则2x=x2,即可判断出;
C.由等轴双曲线的性质即可判断出;
D.由双曲线x2-
=1可得:a=1,b=2,即可得出渐近线方程.
B.取x=2,则2x=x2,即可判断出;
C.由等轴双曲线的性质即可判断出;
D.由双曲线x2-
| y2 |
| 4 |
解答:
解:A.∵?x∈R,则ex>0,∴?x0∈R,ex0≤0不正确;
B.取x=2,则2x=x2,因此?x∈R,2x>x2不正确;
C.∵双曲线x2-y2=1的离心率为
,∴C不正确;
D.双曲线x2-
=1的渐近线方程为y=±2x,正确.
综上可知:只有D正确.
故选:D.
B.取x=2,则2x=x2,因此?x∈R,2x>x2不正确;
C.∵双曲线x2-y2=1的离心率为
| 2 |
D.双曲线x2-
| y2 |
| 4 |
综上可知:只有D正确.
故选:D.
点评:本题考查了指数函数的性质、幂函数的性质、双曲线的标准与性质等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
在平面直角坐标系xOy中,已知
=(-1,t),
=(2,2),若∠ABO=90°,则t=( )
| OA |
| OB |
| A、2 | B、4 | C、5 | D、8 |
设等比数列{an}的前n项和为Sn,若Sm-1=5,Sm=-11,Sm+1=21,则m=( )
| A、3 | B、4 | C、5 | D、6 |
直线y-1=k(x-3)被圆(x-2)2+(y-2)2=4所截得的最短弦长等于( )
A、
| ||
B、2
| ||
C、2
| ||
D、
|
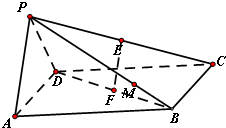 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.