题目内容
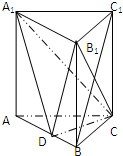 已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点.
已知直三棱柱ABC-A1B1C1中,AC=BC,点D是AB的中点.(1)求证:BC1∥平面CA1D;
(2)求证:平面CA1D⊥平面AA1B1B;
(3)若底面ABC为边长为2的正三角形,BB1=
| 3 |
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)连接AC1交A1C于点E,连接DE,由直三棱柱的几何特征及三角形中位线定理,可得DE∥BC1,进而由线面平行的判定定理得到结论;
(2)先利用面面垂直的性质定理证明直线CD⊥平面AA1B1B,再由面面垂直的判定定理证明所证结论即可
(3)三棱锥B1-A1DC的体积VB1-A1DC=VC-A1B1D,求出棱锥的底面面积和高,代入棱锥体积公式,可得答案.
(2)先利用面面垂直的性质定理证明直线CD⊥平面AA1B1B,再由面面垂直的判定定理证明所证结论即可
(3)三棱锥B1-A1DC的体积VB1-A1DC=VC-A1B1D,求出棱锥的底面面积和高,代入棱锥体积公式,可得答案.
解答:
证明:(1)连接AC1交A1C于点E,连接DE
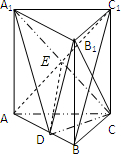
∵四边形AA1C1C是矩形,则E为AC1的中点
又∵D是AB的中点,DE∥BC1,
又DE?面CA1D,BC1?面CA1D,
∴BC1∥平面CA1D;
(2)AC=BC,D是AB的中点,
∴AB⊥CD,
又∵AA1⊥面ABC,CD?面ABC,
∴AA1⊥CD,
∵AA1∩AB=A,
∴CD⊥面AA1B1B,
又∵CD?面CA1D,
∴平面CA1D⊥平面AA1B1B
(3)则由(2)知CD⊥面ABB1B,
∴三棱锥B1-A1DC底面B1A1D上的高就是CD=
,
又∵BD=1,BB1=
,
∴A1D=B1D=A1B1=2,SA1B1D=
,
∴三棱锥B1-A1DC的体积VB1-A1DC=VC-A1B1D=
•
•
=1

∵四边形AA1C1C是矩形,则E为AC1的中点
又∵D是AB的中点,DE∥BC1,
又DE?面CA1D,BC1?面CA1D,
∴BC1∥平面CA1D;
(2)AC=BC,D是AB的中点,
∴AB⊥CD,
又∵AA1⊥面ABC,CD?面ABC,
∴AA1⊥CD,
∵AA1∩AB=A,
∴CD⊥面AA1B1B,
又∵CD?面CA1D,
∴平面CA1D⊥平面AA1B1B
(3)则由(2)知CD⊥面ABB1B,
∴三棱锥B1-A1DC底面B1A1D上的高就是CD=
| 3 |
又∵BD=1,BB1=
| 3 |
∴A1D=B1D=A1B1=2,SA1B1D=
| 3 |
∴三棱锥B1-A1DC的体积VB1-A1DC=VC-A1B1D=
| 1 |
| 3 |
| 3 |
| 3 |
点评:本题主要考查了直棱柱中的线面、面面关系,线面及面面平行、垂直的判定定理和性质定理的应用,棱锥的体积,推理论证的能力和表达能力,注意证明过程的严密性

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
设等比数列{an}的前n项和为Sn,若Sm-1=5,Sm=-11,Sm+1=21,则m=( )
| A、3 | B、4 | C、5 | D、6 |
已知a、b都是实数,a≠0,f(x)=|x-1|+|x-2|.
(1)若f(x)>2,求实数x的取值范围;
(2)若|a+b|+|a-b|≥|a|f(x)对满足条件的所有a、b都成立,求实数x的取值范围.
(1)若f(x)>2,求实数x的取值范围;
(2)若|a+b|+|a-b|≥|a|f(x)对满足条件的所有a、b都成立,求实数x的取值范围.
已知a>1,b>1,且lnalnb=
,则ab( )
| 1 |
| 4 |
| A、有最大值1 |
| B、有最小值1 |
| C、有最大值e |
| D、有最小值e |

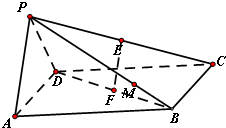 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.