题目内容
4.关于函数y=tan(2x+$\frac{2π}{3}$),下列说法正确的是( )| A. | 是奇函数 | B. | 在区间$(\frac{π}{12},\frac{7π}{12})$上单调递增 | ||
| C. | $(-\frac{π}{12},0)$为其图象的一个对称中心 | D. | 最小正周期为π |
分析 判断函数的周期,求出对称中心,函数的单调性,判断选项即可.
解答 解:函数y=tan(2x+$\frac{2π}{3}$),函数的周期为:$\frac{π}{2}$,
当x=0时,y=-$\sqrt{3}$,函数不是奇函数;
因为kπ$-\frac{π}{2}$$<2x+\frac{2π}{3}$$<kπ+\frac{π}{2}$,k∈Z,解得x∈($\frac{kπ}{2}-\frac{7π}{12}$,$\frac{kπ}{2}-\frac{π}{12}$),k∈Z,
所以在区间$(\frac{π}{12},\frac{7π}{12})$上单调递增,不正确;
x=-$\frac{π}{12}$时,y=tan($\frac{π}{2}$)不存在,所以$(-\frac{π}{12},0)$为其图象的一个对称中心.正确.
故选:C.
点评 本题考查命题的真假的判断,正切函数的单调性、奇偶性、对称性、周期性的求法,考查计算能力.

练习册系列答案
相关题目
15. 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{3}{8}$ |
16.已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如表:
若抽取学生n人,成绩分为A(优秀),B(良好),C(及格)三个等次,设x,y分别表示数学成绩与地理成绩,例如:表中地理成绩为A等级的共有14+40+10=64(人),数学成绩为B等级且地理成绩为C等级的有8人.已知x与y均为A等级的概率是0.07.
(Ⅰ)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(Ⅱ)已知a≥7,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
| 人数 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
(Ⅰ)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(Ⅱ)已知a≥7,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
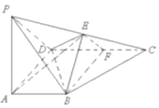 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点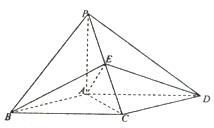 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.