题目内容
1.平面上一机器人在行进中始终保持与点F(1,0)的距离比到直线x=-2的距离小1.若机器人接触不到过点P(-1,0)且斜率为k的直线,则k的取值范围是k<-1或k>1.分析 由抛物线的定义,求出机器人的轨迹方程,过点P(-1,0)且斜率为k的直线方程为y=k(x+1),代入y2=4x,利用判别式,即可求出k的取值范围
解答 解:平面上一机器人在行进中始终保持与点F(1,0)的距离比到直线x=-2的距离小1,
即平面上一机器人在行进中始终保持与点F(1,0)的距离和到直线x=-1的距离相等,
由抛物线的定义可知,机器人的轨迹方程为y2=4x,
过点P(-1,0)且斜率为k的直线方程为y=k(x+1),
代入y2=4x,可得k2x2+(2k2-4)x+k2=0,
∵机器人接触不到过点P(-1,0)且斜率为k的直线,
∴△=(2k2-4)2-4k4<0,
∴k<-1或k>1.
故答案为:k<-1或k>1.
点评 本题考查抛物线的定义,考查直线与抛物线的位置关系,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.平面α∩β=l,直线m?α,直线n?β,则m,n的位置关系是( )
| A. | 异面 | B. | 平行 | C. | 相交 | D. | 无法确定 |
9.设Sn为等比数列{an}的前n项和,记命题甲:4a2-a4=0,命题乙:S4=5S2,则命题甲成立是命题乙成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知$cos({60°}+α)=\frac{1}{3}$,且-180°<α<-90°,则cos(30°-α)的值为( )
| A. | $-\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
6.已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的表面积等于( )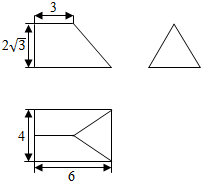

| A. | 60+4$\sqrt{3}$+2$\sqrt{21}$ | B. | 60+2$\sqrt{3}$+2$\sqrt{21}$ | C. | 60+2$\sqrt{3}$+4$\sqrt{21}$ | D. | 60+4$\sqrt{3}$+4$\sqrt{21}$ |
10.已知中心在原点的椭圆C以抛物线y2=4x的焦点F为右焦点,且它们的公共点P到点F的距离为$\frac{5}{3}$,则椭圆C的标准方程为( )
| A. | $\frac{{x}^{2}}{4}$+y2=1 | B. | $\frac{{y}^{2}}{4}$+x2=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |