题目内容
6.已知A、B、C是平面上不共线的三点,O是△ABC的重心,点P满足$\overrightarrow{OP}$=$\frac{1}{4}$($\overrightarrow{OA}$+$\overrightarrow{OB}$+2$\overrightarrow{OC}$),则$\frac{{S}_{△PAB}}{{S}_{△OAB}}$为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
分析 作出图形:延长CO交边AB的中点于D,根据O是△ABC的重心,以及向量加法的平行四边形法则、向量数乘的几何意义和向量的数乘运算便可以得出$\overrightarrow{OP}=\frac{1}{4}\overrightarrow{OC}$,从而便可得到$OP=\frac{1}{6}CD,DP=\frac{1}{2}CD$,而$DO=\frac{1}{3}CD$,这样即可求出$\frac{{S}_{△PAB}}{{S}_{△OAB}}$的值.
解答 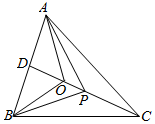 解:如图,延长CO,交AB中点D,O是△ABC的重心,则:
解:如图,延长CO,交AB中点D,O是△ABC的重心,则:
$\overrightarrow{OP}=\frac{1}{4}(\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC})$=$\frac{1}{4}(2\overrightarrow{OD}+2\overrightarrow{OC})$=$\frac{1}{4}(-\overrightarrow{OC}+2\overrightarrow{OC})$=$\frac{1}{4}\overrightarrow{OC}$;
∴$OP=\frac{1}{4}OC=\frac{1}{4}•\frac{2}{3}CD=\frac{1}{6}CD$;
∴$DP=DO+OP=\frac{1}{3}CD+\frac{1}{6}CD=\frac{1}{2}CD$,$DO=\frac{1}{3}CD$;
∴$\frac{{S}_{△PAB}}{{S}_{△OAB}}=\frac{DP}{DO}=\frac{\frac{1}{2}CD}{\frac{1}{3}CD}=\frac{3}{2}$.
故选A.
点评 考查向量加法的平行四边形法则,向量数乘的几何意义,三角形重心的性质,以及向量的数乘运算,三角形的面积公式.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | 0.488 | B. | 0.494 | C. | 0.502 | D. | 0.512 |
| A. | (0,$\frac{π}{4}$) | B. | (0,$\frac{π}{3}$) | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{π}{6}$,$\frac{π}{3}$) |
| A. | -7.2 | B. | 7.2 | C. | -2.32 | D. | 2.32 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{4}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
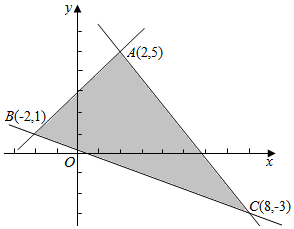 直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示:
直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示: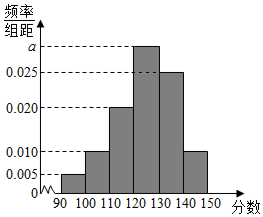 某高校从2015年招收的大一新生中,随机抽取60名学生,将他们的2015年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.
某高校从2015年招收的大一新生中,随机抽取60名学生,将他们的2015年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.