题目内容
2.在($\sqrt{2}$+$\root{4}{3}$)60展开式中,有理项共有16项(用数字作答)分析 根据通项公式可得当$\frac{60-r}{2}$ 和$\frac{r}{4}$都是整数时,才会得到有理项,故r=0,4,8,12,…,60时,得到有理项,从而得出结论.
解答 解:在($\sqrt{2}$+$\root{4}{3}$)60展开式的通项公式为Tr+1=${C}_{60}^{r}$•${2}^{\frac{60-r}{2}}$•${3}^{\frac{r}{4}}$,
故当$\frac{60-r}{2}$ 和$\frac{r}{4}$都是整数时,才会得到有理项,
∴r=0,4,8,12,…,60时,得到有理项,共计16项,
故答案为:16.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.盒中共有形状大小完全相同的5个球,其中有2个红球和3个白球.若从中随机取2个球,则概率为$\frac{3}{5}$的事件是( )
| A. | 都不是红球 | B. | 恰有1个红球 | C. | 至少有1个红球 | D. | 至多有1个红球 |
13.已知f(x)是定义在R上的增函数,函数y=f(x-1)的图象关于点(1,0)对称.若对任意的x,y∈R,不等式f(x2-6x-21)+f(2x)<0恒成立,x的取值范围是( )
| A. | (-3,7) | B. | (-9,2) | C. | ( 3,7) | D. | (2,9) |
7.按下列要求从12人中选出5人参加某项公益动.分别有多少种不同的选法?
(1)甲、乙两人都不入选.
(2)甲、乙两人至多1人入选.
(3)甲、乙、丙3人至少有1人入选.
(4)甲、乙、丙3人至多有2人入选.
(1)甲、乙两人都不入选.
(2)甲、乙两人至多1人入选.
(3)甲、乙、丙3人至少有1人入选.
(4)甲、乙、丙3人至多有2人入选.
11.已知i是虚数单位,则复数$\frac{(1-i)^{2}}{1+2i}$在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
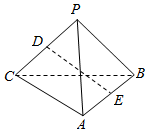 如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
如图,P是平面ABC外一点,PA=4,BC=2$\sqrt{5}$,D,E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.