题目内容
18.已知x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$,若z=a(4x+2y)+b(a>0,b>0)的最大值为7,则$\frac{6}{a}$+$\frac{1}{b}$的最小值为7.分析 由x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$,画出可行域:利用图象可知:当z=a(4x+2y)+b直线过(2,-1)时,z取得最大值7.得到6a+b=7.再利用基本不等式即可得出答案.
解答 解:由x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$,画出可行域: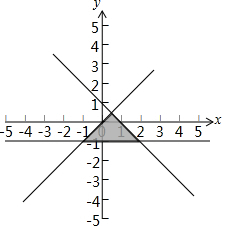
∵a>0,b>0,z=a(4x+2y)+b,
∴y=-2x+$\frac{z-b}{2a}$,其斜率-2<0,在y轴上的截距为$\frac{z-b}{2a}$,
由图象可知:当此直线过点(2,-1)时,z=a(4x+2y)+b取得最大值7.
即6a+b=7.
∴$\frac{6}{a}$+$\frac{1}{b}$=$\frac{1}{7}$($\frac{6}{a}$+$\frac{1}{b}$)(6a+b)=$\frac{1}{7}$(37+$\frac{6b}{a}$+$\frac{6a}{b}$)≥$\frac{1}{7}$(37+2$\sqrt{\frac{6b}{a}•\frac{6a}{b}}$)=7,
当且仅当a=b=1时取等号.
∴$\frac{6}{a}$+$\frac{1}{b}$的最小值为7.
故答案为:7
点评 本题考查了线性规划的有关知识与基本不等式的性质,属于中档题.

练习册系列答案
相关题目
8.若集合A={0,1,2},B={1,2,5},则集合A∩B的子集个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 16 |
13.命题:“若$\sqrt{x}$>1,则lnx>0”的否命题为( )
| A. | 若$\sqrt{x}$>1,则lnx≤0 | B. | 若$\sqrt{x}$≤1,则lnx>0 | C. | 若$\sqrt{x}$≤1,则lnx≤0 | D. | 若lnx>0,则$\sqrt{x}$>1 |
3.双曲线y2-$\frac{{x}^{2}}{7}$=1的渐近线方程为( )
| A. | y=±$\sqrt{7}$x | B. | y=±7x | C. | y=±$\frac{\sqrt{7}}{7}$x | D. | y=±$\frac{1}{7}$x |
10.命题“?x∈R,x3-3x>0”的否定为( )
| A. | ?x∈R,x3-3x≤0 | B. | ?x∈R,x3-3x<0 | C. | ?x∈R,x3-3x≤0 | D. | ?x∈R,x3-3x>0 |
8.已知双曲线的焦点在x轴上,焦距为2$\sqrt{5}$,且双曲线的一条渐近线与直线x-2y+1=0平行,则双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{4}$-y2=1 | B. | x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{3{x}^{2}}{20}$-$\frac{3{y}^{2}}{5}$=1 | D. | $\frac{3{x}^{2}}{5}$-$\frac{3{y}^{2}}{20}$=1 |