题目内容
8.阿基米德在《论球与圆柱》一书中推导球的体积公式时,得到一个等价的三角恒等式sin$\frac{π}{2n}+sin\frac{2π}{2n}+…+\frac{(2n-1)π}{2n}=\frac{1}{{tan\frac{π}{4n}}}$,若在两边同乘以$\frac{π}{2n}$,并令n→+∞,则左边=$\lim_{x→∞}\sum_{i=1}^{2n}{\frac{π}{2n}sin\frac{iπ}{2n}}=\int_0^π{sinxdx}$.因此阿基米德实际上获得定积分$\int_0^π{sinxdx}$的等价结果.则$\int_0^π{sinxdx}$=2.分析 找出被积函数的原函数,代入积分上限和下限解答即可.
解答 解:$\int_0^π{sinxdx}$=(-cosx)${|}_{0}^{π}$=2.
故答案为:2.
点评 本题考查定积分的求法,是基础题,解题时要认真审题,注意定积分的性质的合理运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
1.圆x2+y2=9,以M(2,1)为中点的弦所在的直线方程为( )
| A. | x+2y-4=0 | B. | 4x+y-9=0 | C. | 2x-y-3=0 | D. | 2x+y-5=0 |
3.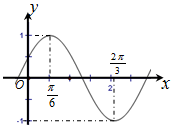 已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )| A. | 1,2,-$\frac{π}{3}$ | B. | 1,$\frac{1}{2}$,-$\frac{π}{3}$ | C. | 1,2,$\frac{π}{6}$ | D. | 1,$\frac{1}{2}$,$\frac{π}{6}$ |
17.若变量x,y满足条$\left\{\begin{array}{l}y≥0\\ x+2y≥1\\ x+4y≤3\end{array}\right.$,则z=(x+1)2+y2的最小值是( )
| A. | 1 | B. | 2 | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{4}{5}$ |