题目内容
16.已知三点A(-1,-1),B(1,x),C(2,5)共线,则x的值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 三点A(-1,-1),B(1,x),C(2,5)共线,可得kAB=kAC,解出即可得出.
解答 解:∵三点A(-1,-1),B(1,x),C(2,5)共线,
∴kAB=kAC,
∴$\frac{x+1}{1+1}$=$\frac{-1-5}{-1-2}$,解得x=3.
故选:C.
点评 本题考查了斜率计算公式、三点共线与斜率的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知集合A,B,C满足A∪B={a,b,c},则满足条件的组合(A,B)共有( )组.
| A. | 4 | B. | 8 | C. | 9 | D. | 27 |
4.与函数y=x是同一函数的函数是( )
| A. | $y=\sqrt{x^2}$ | B. | $y=\root{3}{x^3}$ | C. | $y={(\sqrt{x})^2}$ | D. | $y=\frac{x^2}{x}$ |
11.已知点P(2,1)在圆C:x2+y2+ax-2y+b=0上,点P关于直线x+y-1=0的对称点也在圆C上,则圆C的圆心坐标为( )
| A. | (0,1) | B. | (1,0) | C. | (2,1) | D. | (1,2) |
1.圆x2+y2=9,以M(2,1)为中点的弦所在的直线方程为( )
| A. | x+2y-4=0 | B. | 4x+y-9=0 | C. | 2x-y-3=0 | D. | 2x+y-5=0 |
5.如图所示是一个容量为200的样本的重量频率分布直方图,则由图可估计该样本重量的平均数为( )

| A. | 11 | B. | 11.5 | C. | 12 | D. | 12.5 |
3.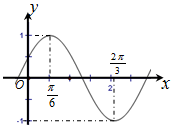 已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )| A. | 1,2,-$\frac{π}{3}$ | B. | 1,$\frac{1}{2}$,-$\frac{π}{3}$ | C. | 1,2,$\frac{π}{6}$ | D. | 1,$\frac{1}{2}$,$\frac{π}{6}$ |
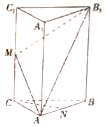 如图,在正三棱柱ABC-A1B1C1中,AB=2,M,N分别是CC1,AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,M,N分别是CC1,AB的中点.