题目内容
11.已知四边形ABCD为正方形,点E是CD的中点,若$\overrightarrow{AB}$=$\vec a$,$\overrightarrow{AD}$=$\vec b$,则$\overrightarrow{BE}$=( )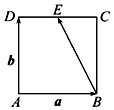
| A. | $\frac{1}{2}$$\vec b$+$\vec a$ | B. | $\vec b$$-\frac{1}{2}$$\vec a$ | C. | $\frac{1}{2}$$\vec a$+$\vec b$ | D. | $\vec a$-$\frac{1}{2}$$\vec b$ |
分析 利用向量的加、减法法则将$\overrightarrow{BE}$用基向量$\overrightarrow{AB}$,$\overrightarrow{AD}$表示出即可.
解答 解:∵四边形ABCD为正方形,E为CD边的中点,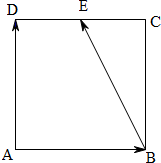
∴2$\overrightarrow{BE}$=$\overrightarrow{BD}$+$\overrightarrow{BC}$=$\overrightarrow{BA}$+$\overrightarrow{AD}$+$\overrightarrow{BC}$,
在正方形ABCD中,$\overrightarrow{BC}$=$\overrightarrow{AD}$,
又∵$\overrightarrow{BA}$=-$\overrightarrow{AB}$,
∴2$\overrightarrow{BE}$=-$\overrightarrow{AB}$+2$\overrightarrow{AD}$=2$\overrightarrow{b}$-$\overrightarrow{a}$,
∴$\overrightarrow{BE}$=$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$,
故选:B.
点评 本题考查了向量的加法原理与向量的减法原理,以及平面向量基本定理.解题的关键是运用向量加法和减法的三角形法则或平行四边形法则,将要求的向量一步一步向已知的向量转化.属于基础题.

练习册系列答案
相关题目
4.与函数y=x是同一函数的函数是( )
| A. | $y=\sqrt{x^2}$ | B. | $y=\root{3}{x^3}$ | C. | $y={(\sqrt{x})^2}$ | D. | $y=\frac{x^2}{x}$ |
5.如图所示是一个容量为200的样本的重量频率分布直方图,则由图可估计该样本重量的平均数为( )

| A. | 11 | B. | 11.5 | C. | 12 | D. | 12.5 |
3.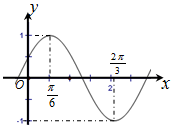 已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )| A. | 1,2,-$\frac{π}{3}$ | B. | 1,$\frac{1}{2}$,-$\frac{π}{3}$ | C. | 1,2,$\frac{π}{6}$ | D. | 1,$\frac{1}{2}$,$\frac{π}{6}$ |
1.已知方程$\frac{x^2}{m-1}+\frac{y^2}{4-m}=1$表示焦点在x轴上的双曲线的一个充分不必要条件是( )
| A. | (4,+∞) | B. | (5,+∞) | C. | $(1,\frac{5}{2})$ | D. | (1,2) |