题目内容
12．若集合M={y|y=$\frac{1}{{x}^{2}}$}，N={x|y=$\sqrt{x-1}$}，那么M∩N=（ ）| A． | （0，+∞） | B． | （1，+∞） | C． | [1，+∞） | D． | [0，+∞） |
分析 先分别求出集合M，N，由此利用交集定义能求出M∩N．
解答 解：∵集合M={y|y=$\frac{1}{{x}^{2}}$}={y＞0}，
N={x|y=$\sqrt{x-1}$}={x|x≥1}，
∴M∩N={x|x≥1}=[1，+∞）．
故选：C．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．
练习册系列答案
相关题目
5．如图所示是一个容量为200的样本的重量频率分布直方图，则由图可估计该样本重量的平均数为（ ）
| A． | 11 | B． | 11.5 | C． | 12 | D． | 12.5 |
3．
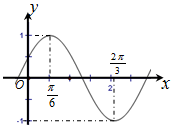已知函数f（x）=Asin（ωx+φ）（A＞0，?＞0，|φ|＜$\frac{π}{2}$）的简图如下，则A，ω，φ分别为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，?＞0，|φ|＜$\frac{π}{2}$）的简图如下，则A，ω，φ分别为（ ）| A． | 1，2，-$\frac{π}{3}$ | B． | 1，$\frac{1}{2}$，-$\frac{π}{3}$ | C． | 1，2，$\frac{π}{6}$ | D． | 1，$\frac{1}{2}$，$\frac{π}{6}$ |
7．若f（x）=ax3+3x2+2，f′（-1）=3，则a的值等于（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 6 |
17．若变量x，y满足条$\left\{\begin{array}{l}y≥0\\ x+2y≥1\\ x+4y≤3\end{array}\right.$，则z=（x+1）2+y2的最小值是（ ）
| A． | 1 | B． | 2 | C． | $\frac{{\sqrt{5}}}{5}$ | D． | $\frac{4}{5}$ |
1．已知方程$\frac{x^2}{m-1}+\frac{y^2}{4-m}=1$表示焦点在x轴上的双曲线的一个充分不必要条件是（ ）
| A． | （4，+∞） | B． | （5，+∞） | C． | $（1，\frac{5}{2}）$ | D． | （1，2） |
2．为了考察某种药物预防禽流感的效果，某研究中心选了50只鸭子做实验，统计结果如下：
（1）能有多大的把握认为药物有效？
（2）在服药后得禽流感的鸭子中，有2只母鸭，3只公鸭，在这5只中随机抽取3只再进行研究，求至少抽到1只母鸭的概率．
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
临界值表：
| 得禽流感 | 不得禽流感 | 总计 | |
| 服药 | 5 | 20 | 25 |
| 不服药 | 15 | 10 | 25 |
| 总计 | 20 | 30 | 50 |
（2）在服药后得禽流感的鸭子中，有2只母鸭，3只公鸭，在这5只中随机抽取3只再进行研究，求至少抽到1只母鸭的概率．
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
临界值表：
| P（K2≥k0） | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |