题目内容

设两个命题p、q，其中p：?x∈R，不等式x2+2x-1＞0恒成立；q：当
3
4
＜a＜1时，函数f（x）=（4a-3）x在R上为减函数，则下列命题为真命题的是（　　）
A、p∧qB、￢p∧￢q
C、￢p∧qD、p∧￢q
考点：复合命题的真假
专题：简易逻辑
分析：先判断出p，q的真假，再判断出复合命题的真假，从而得到答案．
解答： 解：p：?x∈R，不等式x2+2x-1＞0不恒成立，∴命题p是假命题，
q：当
3
4
＜a＜1时，0＜4a-3＜1，函数f（x）=（4a-3）x在R上为减函数，∴命题q是真命题，
∴￢p∧q是真命题，
故选：C．
点评：本题考查了复合命题的判断，考查了不等式以及指数函数的性质，是一道基础题．
练习册系列答案
相关题目
已知凼数f（x）=
3x2+2ax-a-6，x＜0
3x2-(a+3)x+a，x≥0
．
（1）当a=1时，求f（x）的最小值；
（2）若-3≤a≤0且存在三个不同的实数x1，x2，x3，使得f（x1）=f（x2）=f（x3），求证：x1+x2+x3≥-
2
+1．
偶函数f（x）在（-∞，0）∪（0，+∞）上有意义，且在（-∞，0）上是减函数，f（6）=0，设g（θ）=2cos2θ+msinθ-
17
4
m，当g（θ）＜0且f[g（θ）]＞0恒成立时，求m的取值范围．
求导数f（x）=2-2sin2
x
2
．
已知函数f（x）=
x2+2x，x≥0
2x-x2，x＜0
，若f（1-2a2）＞f（a），则实数a的取值范围是
 
．
在△ABC中，A，B，C的对边分别是a，b，c，已知a2+b2=2012c2，求证
2sinAsinBcosC
sin2(A+B)
为定值．
在?ABCD中，AB=2，AD=1，∠DAB=60°，F为DC的中点，E为线段BC上的一个点，若
AE
•
AF
=
15
4
，则
AE
•
AB
=
 
．
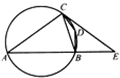如图，四边形么BDC内接于圆，BD=CD，过C点的圆的切线与AB的延长线交于E点．
（I）求证：∠EAC=2∠DCE；
（Ⅱ）若BD⊥AB，BC=BE，AE=2，求AB的长．
已知在平面直角坐标系xoy中，点P（x，y），Q（x，-2），且以线段PQ为直径的圆经过原点O．
（1）求动点P的轨迹C；
（2）过点M（0，-2）的直线l与轨迹C交于两点A、B，点A关于y轴的对称点为A′，试问直线A′B是否恒过一定点，若是，并求此定点；若不是，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网