题目内容
偶函数f(x)在(-∞,0)∪(0,+∞)上有意义,且在(-∞,0)上是减函数,f(6)=0,设g(θ)=2cos2θ+msinθ-
m,当g(θ)<0且f[g(θ)]>0恒成立时,求m的取值范围.
| 17 |
| 4 |
考点:函数恒成立问题,三角函数的最值
专题:函数的性质及应用
分析:根据题意可知,问题可转化为g(θ)<-6对任意的θ恒成立,然后分离参数m,问题转化为三角函数的最值问题.
解答:
解:因为偶函数f(x)在(-∞,0)∪(0,+∞)上有意义,且在(-∞,0)上是减函数,f(6)=0,
所以f(-6)=f(6)=0.
所以若g(θ)<0且f[g(θ)]>0恒成立,则只需g(θ)<-6对任意的θ恒成立即可.
即2cos2θ+msinθ-
m<-6对任意的角θ恒成立.
即2-2sin2θ+msinθ-
m<-6对θ∈R恒成立.
整理得m>
=-[(
-sinθ)+
-17]恒成立.
令t=
-sinθ∈[
,
].
则原式化为m>-[t+
-17],t∈[
,
]①.
令y=t+
,易知该函数在(0,
)上递减,且
>
,
所以y=t+
在[
,
]上递减.
所以t=
时,ymin=-
.
所以要使①式恒成立,只需m>
.
即m的取值范围是(
,+∞).
所以f(-6)=f(6)=0.
所以若g(θ)<0且f[g(θ)]>0恒成立,则只需g(θ)<-6对任意的θ恒成立即可.
即2cos2θ+msinθ-
| 17 |
| 4 |
即2-2sin2θ+msinθ-
| 17 |
| 4 |
整理得m>
| 2sin2θ-8 | ||
sinθ-
|
| 17 |
| 4 |
| ||
|
令t=
| 17 |
| 4 |
| 13 |
| 4 |
| 21 |
| 4 |
则原式化为m>-[t+
| ||
| t |
| 13 |
| 4 |
| 21 |
| 4 |
令y=t+
| ||
| t |
15
| ||
| 4 |
15
| ||
| 4 |
| 21 |
| 4 |
所以y=t+
| ||
| t |
| 13 |
| 4 |
| 21 |
| 4 |
所以t=
| 21 |
| 4 |
| 285 |
| 28 |
所以要使①式恒成立,只需m>
| 285 |
| 28 |
即m的取值范围是(
| 285 |
| 28 |
点评:本题考查了不等式恒成立问题的解题思路,三角函数的最值问题的处理方法,要注意换元思想的应用.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
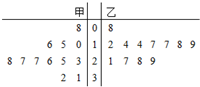 如图是某篮球联赛中,甲、乙两名运动员12个场次得分的茎叶图.设甲、乙两人得分的平均数分别为
如图是某篮球联赛中,甲、乙两名运动员12个场次得分的茎叶图.设甲、乙两人得分的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)=
,则
的值是( )
| x |
| lim |
| △x→0 |
| f(x-△x)-f(x) |
| △x |
A、-
| ||||
B、
| ||||
C、-
|
设两个命题p、q,其中p:?x∈R,不等式x2+2x-1>0恒成立;q:当
<a<1时,函数f(x)=(4a-3)x在R上为减函数,则下列命题为真命题的是( )
| 3 |
| 4 |
| A、p∧q | B、¬p∧¬q |
| C、¬p∧q | D、p∧¬q |
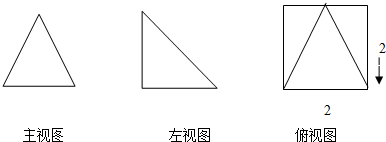
若空间几何体的三视图如图所示,则该几何体体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |