题目内容
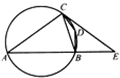 如图,四边形么BDC内接于圆,BD=CD,过C点的圆的切线与AB的延长线交于E点.
如图,四边形么BDC内接于圆,BD=CD,过C点的圆的切线与AB的延长线交于E点.(I)求证:∠EAC=2∠DCE;
(Ⅱ)若BD⊥AB,BC=BE,AE=2,求AB的长.
考点:与圆有关的比例线段,弦切角
专题:推理和证明
分析:(Ⅰ)由等腰三角形性质得∠BCD=∠CBD,由弦切角定理得∠ECD=∠CBD,从而∠BCE=2∠ECD,由此能证明∠EAC=2∠ECD.
(Ⅱ)由已知得AC⊥CD,AC=AB,由BC=BE,得AC=EC.由切割线定理得EC2=AE•BE,由此能求出AB的长.
(Ⅱ)由已知得AC⊥CD,AC=AB,由BC=BE,得AC=EC.由切割线定理得EC2=AE•BE,由此能求出AB的长.
解答:
(Ⅰ)证明:因为BD=CD,所以∠BCD=∠CBD.
因为CE是圆的切线,所以∠ECD=∠CBD.
所以∠ECD=∠BCD,所以∠BCE=2∠ECD.
因为∠EAC=∠BCE,所以∠EAC=2∠ECD.…(5分)
(Ⅱ)解:因为BD⊥AB,所以AC⊥CD,AC=AB.
因为BC=BE,所以∠BEC=∠BCE=∠EAC,所以AC=EC.
由切割线定理得EC2=AE•BE,即AB2=AE•( AE-AB),即
AB2+2 AB-4=0,解得AB=
-1.…(10分)
因为CE是圆的切线,所以∠ECD=∠CBD.
所以∠ECD=∠BCD,所以∠BCE=2∠ECD.
因为∠EAC=∠BCE,所以∠EAC=2∠ECD.…(5分)
(Ⅱ)解:因为BD⊥AB,所以AC⊥CD,AC=AB.
因为BC=BE,所以∠BEC=∠BCE=∠EAC,所以AC=EC.
由切割线定理得EC2=AE•BE,即AB2=AE•( AE-AB),即
AB2+2 AB-4=0,解得AB=
| 5 |
点评:本题考查一个角是另一个角的二倍的证明,考查线段长的求法,是中档题,解题时要认真审题,注意弦切角定理、切割线定理的合理运用.

练习册系列答案
相关题目
设两个命题p、q,其中p:?x∈R,不等式x2+2x-1>0恒成立;q:当
<a<1时,函数f(x)=(4a-3)x在R上为减函数,则下列命题为真命题的是( )
| 3 |
| 4 |
| A、p∧q | B、¬p∧¬q |
| C、¬p∧q | D、p∧¬q |
若空间几何体的三视图如图所示,则该几何体体积为( )
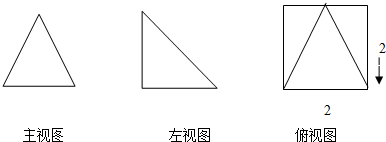

A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |
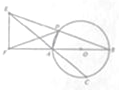 如图所示,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA并交BA的延长线于点F.
如图所示,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA并交BA的延长线于点F.