题目内容
下列概率模型：
① 从区间[－5，5]内任取一个数，求取到1的概率；
② 从区间[－5，5]内任取一个数，求取到绝对值不大于1的数的概率；
③ 从区间[－5，5]内任取一个整数，求取到大于1的数的概率；
④ 向一个边长为5 cm的正方形ABCD内投一点P，求点P离中心不超过1 cm的概率．
其中，是几何概型的有__________．(填序号)
①②④
解析：① [－5，5]上有无限多个数，取到“1”这个数的概率为0，是几何概型；② [－5，5]和[－1，1]上有无限多个数可取(无限性)，且在这两个区间上每个数被取到可能性相同(等可能性)，是几何概型；③ [－5，5]上的整数只有11个，不满足无限性，故不是几何概型；④ 在边长为5 cm的正方形和半径为1 cm的圆内均有无数多个点(无限性)，且这两个区域内的任何一个点都有可能被投到(等可能性)，是几何概型．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ和η，且ξ、η分布列为
| ξ | 1 | 2 | 3 |
| P | a | 0.1 | 0.6 |
| η | 1 | 2 | 3 |
| P | 0.3 | b | 0.3 |
(1) 求a、b的值；
(2) 计算ξ、η的期望和方差，并以此分析甲、乙的技术状况．
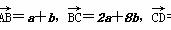＝3(a－b)．求证：A、B、D三点共线；
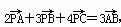，则△PAB与△PBC的面积的比值为__________．