题目内容
6．不等式1+2014x+（1+2015x）2015＞x2015的解集是{x|x＞-$\frac{1}{2014}$}．分析 构造函数f（x）=x2015+x，则函数单调递增，不等式化为1+2015x＞x，即可得出结论．
解答 解：构造函数f（x）=x2015+x，则函数单调递增，
∵1+2014x+（1+2015x）2015＞x2015，
∴1+2015x+（1+2015x）2015＞x2015+x，
∴1+2015x＞x，
∴x＞-$\frac{1}{2014}$，
故答案为{x|x＞-$\frac{1}{2014}$}．
点评 本题考查不等式的解法，考查构造法的运用，正确运用函数的单调性是关键．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
14．
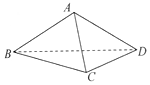如图，在三棱锥A-BCD中，侧面ABD⊥底面BCD，BC⊥CD，AB=AD=4，BC=6，BD=4$\sqrt{3}$，直线AC与底面BCD所成角的大小为（ ）
如图，在三棱锥A-BCD中，侧面ABD⊥底面BCD，BC⊥CD，AB=AD=4，BC=6，BD=4$\sqrt{3}$，直线AC与底面BCD所成角的大小为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由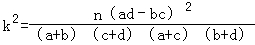
算得，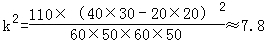
．
P（K2≥k） | 0．050 | 0．010 | 0．001 |
k | 3．841 | 6．635 | 10．828 |
参照附表，得到的正确结论是（ ）
A．在犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别有关”
B．在犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别无关”
C．有99%以上的把握认为“爱好该项运动与性别有关”
D．有99%以上的把握认为“爱好该项运动与性别无关”
，那么cosC等于 （ ）
B.
C.
D.
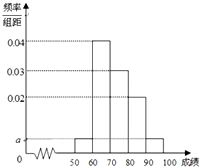某校100名学生期末考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．